2021年人教版八年级数学上册第13章《轴对称》13.4 课题学习——最短路径问题
一、单选题
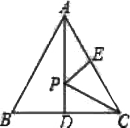
1.在等边三角形ABC 中,D,E分别是BC,AC的中点,点P是线段AD上的一个动点,当△PCE的周长最小时,Р点的位置在( )
A. A点处
B. D点处
C. AD的中点处
D. △ABC三条高的交点处
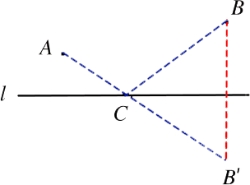
2.如图,点A,B是直线l同侧不重合的两点,在直线l上求作一点C,使得AC+BC的长度最短.作法︰①作点B关于直线的对称点B';②连接AB',与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有用到的知识或方法是( )
A.转化思想
B.三角形两边之和大于第三边
C.两点之间,线段最短
D.三角形的一个外角大于与它不相邻的任意一个内角
4.在平面直角坐标系中,点A、B的坐标分别为(2,0),(4,0),点C的坐标为(m,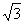 m) (m为非负数),则CA+CB的最小值是( )
m) (m为非负数),则CA+CB的最小值是( )
B.
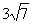
C.
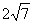
D. 5
二、填空题
此内容正在抓紧时间编辑中,请耐心等待
崔老师
男,中教高级职称
市优秀教师、骨干教师,数学学科带头人。在教学中注重学生自学能力和数学思维能力的培养,教学成绩突出。




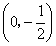
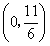
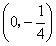
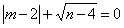 ,且m、n恰好是等腰
,且m、n恰好是等腰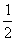 BC,则△ABC的顶角的度数为.
BC,则△ABC的顶角的度数为.