课程内容：

  7.4平行线的判定：

 一：观察与思考

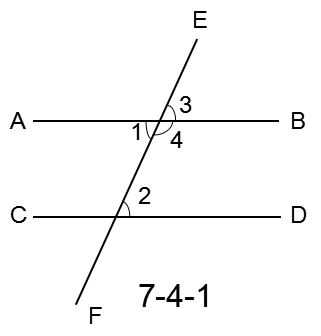
 我们已经知道：同位角相等，两直线平行.即在图7-4-1中，如果∠2=∠3，那么AB∥CD.

  小亮和小红经过认真观察有了新的发现，

  小亮的发现：

因为∠1=∠3（ 对顶角相等）.

如果∠1=∠2，那么就能推出∠2=∠3

，于是就有AB∥CD

小红的发现：因为∠3+∠4=180°（ 平角定义）.

如果∠2+∠4=180°，那么就能推出∠2=∠3，于是就有AB∥CD  （1）你认为小亮和小红

的想法正确吗？

 二：定理：两条直线被第三条直线所截，如果内错角相等（或者同旁内角互补），

那么这两条直线平行.    简单的说就是：内错角相等，两直线平行.

同旁内角互补，两直线平行。 

三：例题   

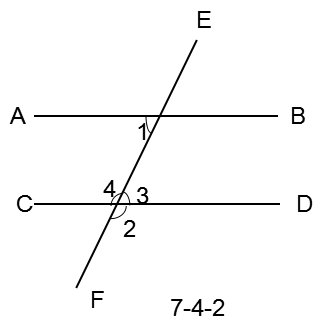
 如图7-4-2,已知：如图7-4-2，直线AB，CD被直线EF

所截，∠1=60°，∠2=120°.

对AB∥CD说明理由。

    理由：

∵∠1+∠2=60°+120°=180°（已知）

    ∠2=∠4 （对顶角相等），

    ∴ ∠1+∠4=180°（等量代换）

    ∴AB∥CD(同旁内角互补，两直线平行）

  四：你学会了吗？试一试。

   1、如图，直线a,b被直线c所截，如果同位角∠1=∠5，请你写出图中其他相等的

同位角、所有相等的内错角、所有相等的同旁内角.

   2、对于上面例题中的命题，请你试着写出用“内错角相等，两直线平行”或“

同位角相等，两直线平行”进行说理过程.

 五：

  平行线的判定： 同位角相等，两直线平行．

　               内错角相等，两直结平行．

　　             同旁内角互补，两直线平行