课程内容
七年级数学下册第14章《位置与坐标》14.2 平面直角坐标系
什么是数轴?
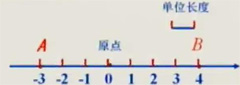
在直线上规定了原点、正方向、单位长度就构成了数轴。
数轴上的点可以用一个数来表示。这个数叫做这个点的坐标。例如点A在数轴上的坐标为-3.点B在数轴上的坐标为4.反过来,知道数轴上一个点的坐标,这个点在数轴上的位置也就确定了。
如何确定一个点在平面内的位置呢?
我们已经知道平面内的点的位置可用有序数对来刻画,能利用数轴解决这一问题吗?
在平面内画出两条互相垂直而且有公共原点的数轴,水平的一条叫x轴或横轴,习惯上取向右的方向为正方向,铅直的一条叫做y轴或纵轴,取向上的方向为正方向,这样就组成了平面直角坐标系,简称直角坐标系。
x轴与y轴统称坐标轴,它们的公共原点叫做坐标原点,简称原点,一般用O表示。
建立直角坐标系
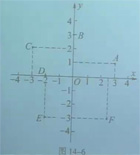
你能用上面的方法,写出图14-6中A,B,C,D,E,F各点的坐标吗?
A(3,1) B(0,3) C(-3,2) D(-2.0) E(-2,-3) F(2.5,-3)
在直角坐标系中,已知一个点的坐标,如何描出这个点呢?
例1、在直角坐标系中,描出下列各点:A(-3,2),B(4,-1),C(-2,-3.5),D(1,3)。
思考:每个象限内的点具有什么特点?
拓展延伸:横纵坐标轴上的点各具备什么特点?
总结提高
原点的坐标为(0,0)
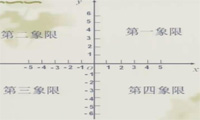
第一象限(+,+)第二象限(-,+)
第三象限(-,-)第四象限(+,-)
任何一个在x轴上的点的纵坐标都为0,记作(x,0).
任何一个在y轴上的点的横坐标为0,记作(0,y).
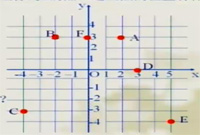
1、如图,在平面直角坐标系中:
(1)写出A,B,C,D,E,F,O各点的坐标。
(2)在以上各点中,找出横坐标为O的点,这些点的位置有什么特点?
(3)在以上各点中,找出纵坐标为O的点,这些点的位置有什么特点?
(4)在以上各点中,纵坐标为3的点有哪几个?连接这几个点的直线与x轴有什么位置关系?
分别说出点A(6,2),B(-3,-1),C(-2,4),D(2,-4)在直角坐标系中所在的象限,并在坐标系中分别描出这些点。
随堂练习
1、点P(-2,3)在第几象限?它到x轴和y轴的距离分别是多少?点Q(3,-2)呢?
总结,对于坐标平面内的任何一个点|x,y|,它到x轴的距离为|y|,它到y轴的距离为|x|
2、在平面直角坐标系内,如果一个点的纵坐标与横坐标同号,它可能在第几象限?如果一个点的纵坐标与横坐标异号,它可能在第几象限?如果至少有一个坐标是0呢?
思维拓展
1、在y轴上,到原点的距离为2的点的坐标是(0,2)或(0,-2)
2、在直角坐标系中,点A(a,0)的位置在x轴上。
3、如果点P(a,b)在第三象限,那么Q(-a,-b)在第一象限。
4、如果点P(m-3,2+m)在x轴上,那么点P的坐标是______.
课堂小结
通过这节课的学习,你有哪些收货?
1.如何建立平面直角坐标系。
2.根据坐标描出点的位置,由点的位置确定点的坐标。
3.知道象限内坐标轴上点的坐标的特点。