课程内容
七年级数学下册第8章《角》回顾与总结（1）
一、角平分线的定义及性质
角平分线定义：从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫这个角的平分线。
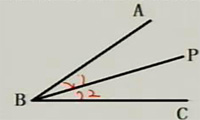
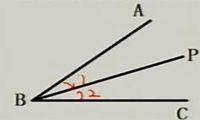
∵BP平分∠ABC
∴∠1=∠2
∠1=1/2∠ABC
（∠2=1/2∠ABC）
∠ABC=2∠1
∠ABC=2∠2
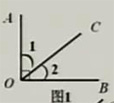
1、如图，BP是∠ABC的角平分线，∠ABC=40°，则∠ABP=20°.
∵BP是∠ABC的平分线
∴∠ABP=1/2∠ABC
=1/2×40°
=20°
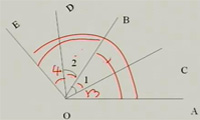
2、如图：OC、OD分别是∠AOB、∠BOE的平分线，
（1）如果∠AOB=70°，∠BOE=60°，那么∠1+∠2=65°
（2）如果∠1+∠2=55°，则∠AOE=110°
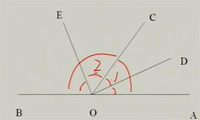
3.如图，点O在直线AB上，OD、OE分别是∠AOC、∠BOC的平分线，则∠EOD=90°
二、余角、补角的定义及性质
余角和补角的定义
如果两个角的和是90°，那么这两个角互为余角，简称“互余”。
同角或等角的余角相等。
如果两个角的和是180°，那么这两个角互为补角，简称“互补”。
同角或等角的补角相等。
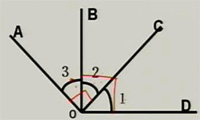
1、如图，∠AOC=90°，∠BOD=90°，则∠1与∠3的关系相等，其理由是同角的余角相等。
2、如图，∠1+∠2=180°，∠3+∠4=180°，若∠1=∠3，则∠2与∠4的关系是相等，其理由是等角的补角相等。
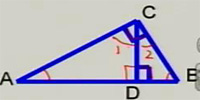
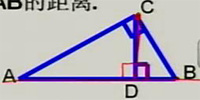
3、如图，∠ACB=90°，CD⊥AB于点D，则∠A=∠2，∠B=∠1.
三、垂线段的定义及性质
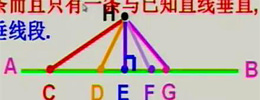
性质1、经过一点有且只有一条直线与已知直线垂直。
性质2：连接直线外一点与直线上各点的所有线段中，垂线段最短。
简记为：垂线段最短。
1、如图已知AC⊥BC，CD⊥AB，则图中AC的长度表示A点到BC的距离；BC的长度表示B点到AC的距离；CD的长度表示C点到AB的距离.
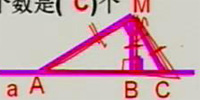
2.如图A，B,C三点在直线a上，M点在直线a外，AM⊥CM，MB⊥AC，在（1）MA>MB（2）MB>MC（3）MC>BC（4）AC>AM这四个结论中，正确的个数是（C）个。
A.1 B.2 C.3 D.4
四、有关垂直、对顶角、余角、补角、角平分线的计算
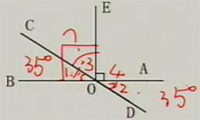
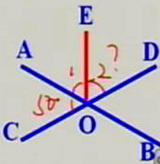
1、直线AB、CD相交于点O，EO⊥AB于点O，如果∠AOD=35°，那么∠EOC等于多少度？
解：∵OE⊥AB于点O
∴∠EOB=90°
∵∠1=∠2=35°
∴∠3=∠EOB-∠1
=90°-35°
=55°
答：∠EOC等于55度。
2、直线AB、CD交于点O，OE是∠AOD的平分线，已知∠AOC=50°。求∠DOE的度数。
解：∠A0D=180°-∠AOC
=180°-50°
=130°
∵OE平分∠AOD
∴∠2=1/2∠AOD
=1/2×130°
=65°
答：∠DOE的度数为65°。
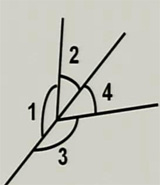
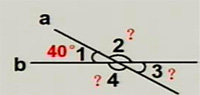
3、如图，直线a、b相交，若∠1=40°，求∠2、∠3、∠4的度数。
解：由邻补角的定义，∠1=40°可得
∠2=180°-∠1
=180°-40°
=140°
由对顶角相等，可得
∠3=∠1=40°
∠4=∠2=140°
变式1：若∠2是∠1的3倍，求∠3的度数？
变式2：若∠2-∠1=40°，求∠4的度数？
此内容正在抓紧时间编辑中，请耐心等待
李老师
女，中教高级职称
热爱教师这个职业，以桃李满天下为荣。积极学习，热情工作，把新的教学理念带入课堂，师生和谐，教学相长。
