课程内容
七年级数学下册第8章《角》8.4 对顶角
如果两条直线有一个公共点,就说这两条直线相交,公共点叫做这两条直线的交点。
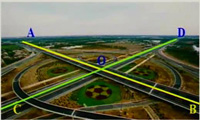
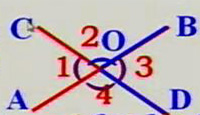
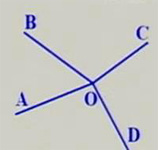
直线AB、CD相交于点O
探究发现
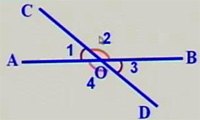
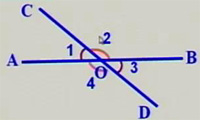
如图:直线AB、CD相交于点O.
(1)如果不计图中的平角和周角,它们共形成了几个角?
(2)这些角的顶点具有什么特征?
(3)观察∠1和∠3,你发现它们的两边具有什么特征?∠2与∠4呢?
形如∠1与∠3有一个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角。
图中还有哪些角也是对顶角呢?
对顶角:如果两个角有一个公共点,并且其中一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角。
注意以下两点:
(1)辨认对顶角的要领:一看是不是两条直线相交所成的角,对顶角与相交线是唇齿相依,哪里有相交直线,哪里就有对顶角,反过来,哪里有对顶角,哪里就有相交线;二看是不是有公共顶点;三看是不是有公共边,符合这三个条件时,才能确定这两个角是对顶角,只具备一个或两个条件都不行。
(2)对顶角是成对存在的,它们是互为对顶角,如∠1是∠3的对顶角,同时,∠3是∠1的对顶角,也常说∠1和∠3是对顶角。
探究发现
∠1与∠3在数量上又有什么关系呢?
对顶角相等
对顶角的性质:对顶角相等。
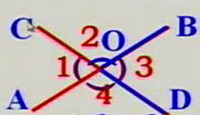
已知:直线AB与CD相交于O点(如图)
求证:∠1=∠3,∠2=∠4
证明:∵直线AB与CD相交于O点,
∴∠1+∠2=180°
∠3+∠2=180°
∴∠1=∠3
同理可得:∠2=∠4
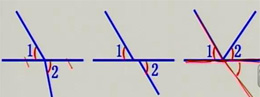
练习1、下列各图中∠1、∠2是对顶角吗?为什么?
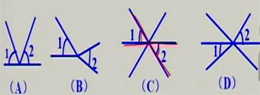
2、下列图形中,∠1和∠2是对顶角的图形是()
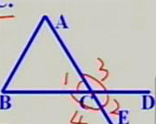
3、如图,已知直线AE、BD相交于点C.图中哪些角是对顶角?
答:对顶角有两对:∠ACB与∠ECD、∠ACD与∠ECB.
4.下列说法是否正确?为什么?
(1)有公共顶点的两个角是对顶角。
答:不正确。如图,∠AOB与∠COD有公共顶点O,但它们不是对顶角。
(2)有公共顶点而没有公共边的两个角是对顶角。
答:不正确。如上图,∠AOB与∠COD有公共顶点O,而且没有公共边,但它们不是对顶角。
例题讲解
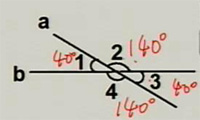
例1:如图,直线a、b相交,若∠1=40°,求∠2、∠3、∠4的度数。
解:∠1=40°,根据题意可得
∠2=180°-∠1
=180°-40°
=140°
由对顶角相等,可得
∠3=∠1=40°
∠4=∠2=140°
若∠1=m°,求各角的度数。
若∠1+∠3=50°,求各角的度数。
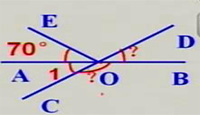
例2、已知:直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,求∠BOD和∠BOC的度数。
解:∵OA平分∠EOC,∠EOC=70°,
∴∠1=1/2∠EOC=1/2×70°=35°,
∴∠BOD=∠1=35°(对顶角相等)
∠BOC=180°-∠BOD
=180°-35°
=145°
答:∠BOD=35°,∠BOC=145°.
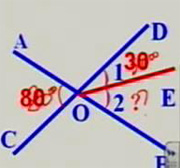
例3、如图,直线AB、CD相交于O,∠AOC=80°,∠1=30°;求∠2的度数。
解决问题
如图,小明想要测量他家房子两堵墙的角度,可他不知道怎么测量,你能帮他解决这个问题吗?
归纳小结
| 角的名称 |
特征 |
性质 |
| 对顶角 |
(1)有公共顶点;
(2)两条边互为反向延长线; |
对顶角相等 |