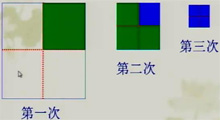
| 次数 | 1 | 2 | 3 | 4 | 5 | ... | |
| 纸片数 | 4 | 7 | 10 | 13 | 16 | ... |

| x | 1 | 2 | 3 |
| 2x-2 | 0 0 | 2 2 | 4 4 |
| x+1 | 2 2 | 3 3 | 4 4 |
| 估计x的值 | 左边 | 与右边64比较 | |
| 第一次估算 | 10 | 31 | 小 |
| 第二次估算 | 20 | 61 | 小 |
| 第三次估算 | 21 | 64 | = |
此内容正在抓紧时间编辑中,请耐心等待
张老师
女,中教高级职称
优秀教师,市级骨干教师、“教学标兵”、劳动模范,市数学教学与研究科研组带头人,注重教学改革与实践。

| 次数 | 1 | 2 | 3 | 4 | 5 | ... | |
| 纸片数 | 4 | 7 | 10 | 13 | 16 | ... |

| x | 1 | 2 | 3 |
| 2x-2 | 0 0 | 2 2 | 4 4 |
| x+1 | 2 2 | 3 3 | 4 4 |
| 估计x的值 | 左边 | 与右边64比较 | |
| 第一次估算 | 10 | 31 | 小 |
| 第二次估算 | 20 | 61 | 小 |
| 第三次估算 | 21 | 64 | = |
此内容正在抓紧时间编辑中,请耐心等待
张老师
女,中教高级职称
优秀教师,市级骨干教师、“教学标兵”、劳动模范,市数学教学与研究科研组带头人,注重教学改革与实践。

七年级数学上册第7章《一元一次方程》7.4 一元一次方程的应用(第五课时)

七年级数学上册第7章《一元一次方程》7.4 一元一次方程的应用(第四课时)

七年级数学上册第6章《整式的加减》回顾与总结(1)

七年级数学上册第6章《整式的加减》6.4 整式的加减(2)

七年级数学上册第6章《整式的加减》6.3 去括号(2)

七年级数学上册第5章《代数式与函数的初步认识》回顾与总结

七年级数学上册第7章《一元一次方程》7.4 一元一次方程的应用(1)

七年级数学上册第7章《一元一次方程》7.3 一元一次方程的解法(第二课时)

七年级数学上册第7章《一元一次方程》7.3 一元一次方程的解法(第一课时)
 正在播放
正在播放
七年级数学上册第7章《一元一次方程》7.2 一元一次方程

七年级数学上册第7章《一元一次方程》7.4 一元一次方程的应用(3)

七年级数学上册第7章《一元一次方程》7.4 一元一次方程的应用(2)

七年级数学上册第6章《整式的加减》回顾与总结(2)

七年级数学上册第2章《有理数》2.3 相反数与绝对值(2)

七年级数学上册第1章《基本的几何图形》回顾与总结

七年级数学上册第6章《整式的加减》6.2 同类项(2)

七年级数学上册第6章《整式的加减》6.2 同类项(1)
七年级数学上册第6章《整式的加减》6.1 单项式与多项式

七年级数学上册第4章《数据的收集、整理与描述》4.4 扇形统计图(第二课时)

七年级数学上册第7章《一元一次方程》7.1 等式的基本性质
评论
点此登录 后即可畅所欲言