课程内容
七年级数学上册第7章《一元一次方程》7.4 一元一次方程的应用（2）
| 星期日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 |
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
2011年12月
创设情境
若某天和它上、下相邻日期的和是42，那么这天是几号呢？
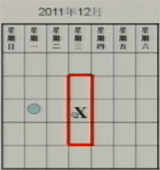
根据题意，口答下列问题
（1）设中间一个数为x，则其他两个数为_x-7___,__x+7__.
（2）题目中的等量关系是_三天的数字之和是42________；
（3）根据相等关系，列出方程__（x-7)+x+(x+7)=42_______。
例2.甲乙两个仓库共存化肥40吨。如果甲仓库运进化肥3吨，乙仓库运出化肥5吨，两仓库所存化肥的质量恰好相等，那么原先两仓库共存化肥多少吨？
如果用x吨表示原来甲仓库库存化肥的质量，填写下表。
| 甲仓库库存化肥质量/吨 | 乙仓库库存化肥质量/吨 | |
| 原来 | x | 40-x |
| 现在 | x+3 | (40-x）-5 |
解：设原来甲仓库库存化肥x吨，则乙仓库库存化肥（40-x）吨。根据题意，得
x+3=(40-x)-5
解这个方程，得
x=16
经检验，x=16(吨)符合题意。
所以，甲乙两仓库原来分别库存化肥16吨和24吨。
还有其他解法吗？
另一种解法：
如果设甲仓库变化后库存化肥x吨。
等量关系是：
甲乙两个仓库共存化肥=40吨
列出方程（x-3)+(x+5)=40
以上两种解法在设未知数和寻找等量关系时有什么不同？
练习二
水上公园某一天共售出门票128张，收入912元。门票价格为成人每张10元，学生可享受六折优惠。这一天出售的成人票与学生票各多少张？
解：设这一天出售的成人票x张，那么学生票售出（128-x)张。根据题意，得
10x+10×60%(128-x)=912
解的 x=36
128-x=92
答：这一天出售的成人票36张，学生票92张。
大小两台拖拉机共耕了5公顷土地。已知大拖拉机的效率是小拖拉机的1.5倍，两台拖拉机各耕地多少公顷？
参加义务劳动，甲地有27人，乙地有19人，现在又派20人去支援两地，使甲地人数是乙地人数的2倍，应去甲地多少人？应去乙地多少人？
分析：如果去甲地x人，那么应去乙地__人，现在甲地有___人，乙地有___人。
解：设应去甲地x人，那么应去乙地(20-x)人。根据题意，得
27+x=2(19+20-x)
x=17
20-x=3
挑战自我
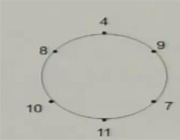
6人围城一圈，每人心中想一个数，并把这个数告诉左、右相邻的人。然后每个人把左、右两个相邻的人告诉自己的数的平均数亮出来（如图）。问亮出11的人原来心中想的数是几？
解：设亮出11的人心中想的数为x，那么亮出9的人心中想的数为14-x，亮出8的人心中想的数为20-x，根据题意，得
（20-x)+(14-x)=2×4
解得 x=13
答：亮出11的人心中想的数为13.
此内容正在抓紧时间编辑中，请耐心等待
张老师
女，中教高级职称
优秀教师，市级骨干教师、“教学标兵”、劳动模范，市数学教学与研究科研组带头人，注重教学改革与实践。
