课程内容
九年级数学上册第4章《一元二次方程》4.5 一元二次方程根的判别式
第四章《一元二次方程》
4.5 一元二次方程根的判别式
实验与探究
(1)你会解方程x²+2x+5=0吗?试一试.
x²+2x+5=0
解:
x²+2x+1=-5+1
(x+1)²=-4
a=1 b2 c=5
b²-4ac=2²-4×1×5=-16<0
(2)由4.3节我们知道,当b²-4ac≥0时,一元二次方程
ax²+bx+c=0 ①
可以利用求根公式
求出它的根.
你发现当b²-4ac>0与b²-4ac=0时,方程的两个根分别具有什么特征?
当b²-4ac>0时,由于
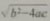
是正数,-
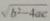
是负数,所以

是两个不相等的实数.因此,方程①有两个不相等的实根:
如果b²-4ac=0,那么
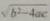
,这时方程①有两个相等的实根:
x1=x2=-b/2a
如果b²-4ac<0,将方程①配方后,得
(x+b/2a)²=b²-4ac/4a²
方程右边由于分母4a²>0,所以b²-4ac/4a²<0,而(x+b/2a)²不可能是负数,这时方程①没有实根.
由此可见,一元二次方程ax²+bx+c=0是否有实根,有实根时两个实根是否相等,均取决于一个含有该方程各项系
数的代数式b²-4ac的值的符号,因而把b²-4ac叫做一元二次方程ax²+bx+c=0的根的判别式(discriminant),通
常用△表示,即△=b²-4ac.
把上面讨论所得到的结论加以归纳,就得到
一元二次方程
ax²+bx+c=0
当△>0时有两个不相等的实根;当△=0时有两个相等的实根;当△<0时没有实根.
上面结论的逆命题也是正确的,你能说出它的逆命题吗?
例1 不解方程,判断下列方程根的情况:
(1)2x²+x-4=0;
(2)4y²+9=12y;
(3)5(t²+1)-6t=0.
解
(1)这里a=2,b=1,c=-4.
∵△=b²-4ac=1²-4×2×(-4)=33>0
∴方程有两个不相等的实根.
(2)把原方程化为一般形式,得
4y²-12y+9=0
这里 a=4,b=-12,c=9
∵△=b²-4ac=(-12)²-4×4×9=0.
∴原方程有两个相等的实根.
(3)把原方程化为一般形式,得
5t²-6t+5=0
这里 a=5,b=-6,c=5
∵△=b²-4ac=(-6)²-4×5×5=-64<0
∴原方程没有实根.
例2 已知关于x的一元二次方程 kx²-3x+1=0
有两个不相等的实根。
(1)求k的取值范围;
(2)选择一个k的正整数值,并求出方程的根.
解
(1)∵关于x的一元二次方程 kx²-3x+1=0
有两个不相等的实根.
∴△=(-3)²-4k>0
即 9-4k>0
解不等式,得k<9/4.
∵kx²-3x+1=0是一元二次方程,
∴k≠0
故k的取值范围是k<9/4且k≠0.
(2)取不等式k<9/4的一个正整数解k=2,则方程为
2x²-3x+1=0
解这个方程,得
x1=1,x2=1/2
挑战自我
有一边长为3的等腰三角形,它的另两边长分别是关于x的方程
x²-12x+k=0
的两根,求k的值.
(1)当3为腰时,k=27.
(2)当3为底时,△=0,k=36.
练习
1.不解方程,判断下列方程根的情况:
(1)3y²-5y-2=0; (2)2x²-9x+6=0;
(3)5x²+10x+6=0;(4)5t²-

+3=0.
2.k为何值时,关于x的一元二次方程
3x²-4x+(k+1)=0
有两个相等的实根?
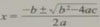
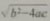 是正数,-
是正数,-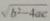 是负数,所以
是负数,所以 是两个不相等的实数.因此,方程①有两个不相等的实根:
是两个不相等的实数.因此,方程①有两个不相等的实根: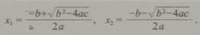
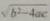 ,这时方程①有两个相等的实根:
,这时方程①有两个相等的实根: +3=0.
+3=0.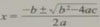
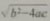 是正数,-
是正数,-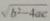 是负数,所以
是负数,所以 是两个不相等的实数.因此,方程①有两个不相等的实根:
是两个不相等的实数.因此,方程①有两个不相等的实根: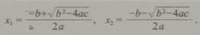
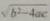 ,这时方程①有两个相等的实根:
,这时方程①有两个相等的实根: +3=0.
+3=0.