课程内容
九年级数学上册第4章《一元二次方程》4.2 用配方法解一元二次方程(第二课时)
第四章《一元二次方程》
4.2 用配方法解一元二次方程
第二课时
例2 解4.1节问题(3)中的方程x²+x-1=0(精确到0.001).
解:
移项,得x²+x=1.
两边都加上(1/2)²,得x²+x+(1/2)²=1+(1/2)²,
(x+1/2)²=5/4.
由平方根的意义,得
x+1/2=±

所以
在4.1节问题(3)中,x为线段AC与AB的比,必须满足x>0.所以x2不合题意.应当舍去。问题(3)的答案是:
AC/AB的值约为0.618。
例3 解方程 2x²+3x-1=0.
方程两边同时除以2,得x²+3/2x-1/2=0.
移项,得x²+3/2x=1/2.
两边都加上(3/4)²,得
x²+3/2x+(3/4)²=1/2+(3/4)².
即 (x+3/4)²=17/16
由平方根的意义,得
x+3/4=±
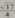
.
所以
挑战自我
如果p与q都是常数,且p²≥4q,你会用配方法解有关x的一元二次方程x²+px+q=0吗?试一试.
练习
1.用配方法解下列方程:
(1)3x²-6x=0; (2)2x²-4x-3=0;
(3)2x²-7x+3=0;(4)4x²-7x-2=0.
2.用配方法证明:
(1)a²-a+1的值恒为正;
(2)多项式2

-4x²-1的值总大于
 -2x²-4的值。
-2x²-4的值。(1)a²-a+1
=a²-a+1/4-1/4+1
=(a-1/2)²+3/4
(a-1/2)²+3/4>0
∴a²-a+1恒为正.
(2)


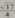 .
.
 -4x²-1的值总大于
-4x²-1的值总大于 -2x²-4的值。
-2x²-4的值。


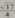 .
.
 -4x²-1的值总大于
-4x²-1的值总大于 -2x²-4的值。
-2x²-4的值。