课程内容
九年级数学上册第3章《对圆的进一步认识》3.6 弧长及扇形面积的计算
第三章《对圆的进一步认识》
3.6 弧长及扇形面积的计算
交流与发现
已知圆的半径为r.思考下面的问题:
(1)圆周上1°弧的长度是整个圆周长的多少?怎样用圆的半径r表示1°弧的长度呢?
(2)由(1),怎样用圆的半径r表示n°弧的长度l呢?与同学交流.
l=nπr/180.
(3)在⊙O中,圆心角为1°的扇形的面积是整个圆面积的多少?怎样用圆的半径r表示圆心角为1°的扇形的面积呢?
(4)由(3),怎样用圆的半径r表示圆心角为n°的扇形面积S扇形呢?
S扇形=nπr²/360.
(5)如果已知⊙O的半径r和扇形的弧长l,怎样用l与r表示这段弧所在的扇形的面积呢?
因为扇形的弧长l=nπr/180.所以nπr²/360=1/2(nπr/180)r,于是
S扇形=1/2lr.
例1
如图3-50所示为一段弯形管道,其中心线是一段圆弧
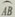
.已知的圆心为O,半径OA为60cm,∠AOB=108°,求这段弯
管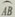 的长度(精确到0.1cm).
的长度(精确到0.1cm).
解
由图3-50可知,n=180°,r=60cm,
代入弧长公式,得
l=nπr/180=108×60π/180≈113.1(cm).
所以,这段弯管的长度约为113.1cm.
例2
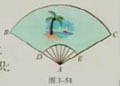
如图3-51,一把扇形纸扇完全打开后,外侧两竹条AB与AC的夹角为120°.AB的长为30cm,竹条AB上贴纸部分BD
的宽为20cm.求扇子的一面上贴纸部分的面积(精确到0.1cm²).
解
由图3-51可知,扇形的圆心为A,圆心角n=120°,AB=30cm.BD=20cm,图上贴纸部分的面积等于两个扇形面积的
差.由扇形的面积公式,贴纸部分的面积为
S扇形BAC-S扇形DAE=nπ·AB²/360-nπ·AD²/360
=120π×30²/360-120π×(30-20)²/360=1/3π(30²-10²)≈837.8(cm²).
所以,扇子的一面上贴纸部分的面积约为837.8cm².
挑战自我
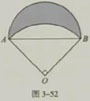
已知扇形AOB的半径r,∠AOB=90°,以弦AB为直径作半圆,得到图3-52.你会求图中“新月形”(阴影部分)
的面积吗?试一试.
练习
1.如图,桥拱的形状是一段圆弧,桥拱

的度数是90°,半径OA为30m.求桥拱
 的长(精确到0.1m).
的长(精确到0.1m).
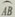 .已知的圆心为O,半径OA为60cm,∠AOB=108°,求这段弯
.已知的圆心为O,半径OA为60cm,∠AOB=108°,求这段弯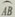 的长度(精确到0.1cm).
的长度(精确到0.1cm).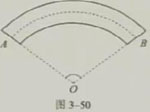
 的度数是90°,半径OA为30m.求桥拱
的度数是90°,半径OA为30m.求桥拱 的长(精确到0.1m).
的长(精确到0.1m).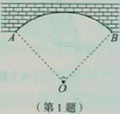
 .已知的圆心为O,半径OA为60cm,∠AOB=108°,求这段弯
.已知的圆心为O,半径OA为60cm,∠AOB=108°,求这段弯 的长度(精确到0.1cm).
的长度(精确到0.1cm).


 的度数是90°,半径OA为30m.求桥拱
的度数是90°,半径OA为30m.求桥拱 的长(精确到0.1m).
的长(精确到0.1m).