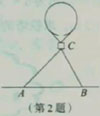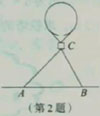课程内容
九年级数学上册第2章《解直角三角形》2.5 解直角三角形的应用(第三课时)
第二章 解直角三角形
2.5 解直角三角形的应用
第三课时
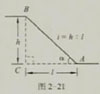
在修路、筑坝、开渠和挖河时,都会遇到修筑斜坡的问题.如图2-21是一段斜坡的横截面,建筑学中把斜坡起止
点A,B的高度差h与它们的水平距离l的比叫做坡度(或坡比),通常用字母i表示,即
i=h:l
如果把图2-21中斜坡AB与水平线AC的夹角记作a,那么表示坡度时,一般把比的前项取作l,如i=l:5.
i=h/l=tana.
这就是说,坡度等于锐角a的正切.
例4
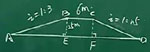
某地计划在河流的上游修建一条拦水大坝,大坝的横截面ABCD是梯形(图2-22),坝顶宽BC=6m,坝高25m,迎
水坡AB的坡度i=l:25.
(1)求斜坡AB和CD的长(精确到0.01m);
(2)求拦水大坝的底面AD的宽.
解
(1)作BE⊥AD,CF⊥AD.垂足分别为点E,F.在Rt△ABE中.∠AEB=90°,BE=25m.
由tanA=BE/AE=1/3,得AE=3BE=3×25=75(m).
∴

在Rt△CDF中,∠CFD=90°,CF=25(m).
由tanD=CF/DF=1/2.5,得DF=2.5CF=2.5×25=62.5(m).
所以

(2)AD=AE+EF+FD=75+6+62.5=143.5(m).
所以,斜坡AB的长约为79.06m,CD的长约为67.31m;水坝的底面宽AD为143.5m.
你还有其他解法吗?与同学交流.
例5
如图2-23,要测量铁塔的高AB,在地面上选取一点C,在A,C两点间选取一点D,测得CD=14m,在C,D两点处分别用
测角仪测得铁塔顶端B的仰角为a=30°和β=45°.测量仪支架的高为1.2m,求铁塔的高(精确到0.1m).
解
由图2-23可知,A₁A=C₁C=D₁D=1.2m,CD=C₁D₁=14m.
∠BC₁A₁=∠a=30°,∠BD₁A₁=∠β=45°.
在Rt△A₁C₁B中,∠BA₁C₁=90°,设A₁B=xm.
由tana=A₁B/A₁C₁,得A₁C₁=A₁B/tana=x/tan30°.
在Rt△A₁D₁B中,由tanβ=A₁B/A₁D₁,得A₁D₁=A₁B/tanβ=s/tan45°.
∵A₁C₁-A₁D₁=C₁D₁.
∴x/tan30°-x/tan45°=14.
解关于x的方程,得x=14·tan30°·tan45°/tan45°-tan30°.
用计算器计算,得x≈19.1,
即A₁B≈19.1m.
∴AB=AA₁-A₁B=1.2+19.1=20.3(m)
练习
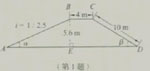
1.如图,拦水坝的横截面为梯形ABCD,根据图中数据,求:
(1)角a和β的大小(精确到1´);
(2)坝底宽AD和斜坡AB的长(精确到0.1m).
2.如图,从地面上相距150m的A,B两点观察空中在C点处的热气球的吊舱,分别测得仰角是42°和65°,试求C点
距离地面的高度(精确到0.1m).
3.如图,为了治理水土流失,计划在山坡上植树,要求相邻两棵树间的水平距离是4.5m,测得斜坡的倾斜角是
20°34´,求斜坡上相邻两棵树间的坡面距离是多少(精确到0.1m).