
此内容正在抓紧时间编辑中,请耐心等待
崔老师
男,中教高级职称
市优秀教师、骨干教师,数学学科带头人。在教学中注重学生自学能力和数学思维能力的培养,教学成绩突出。








此内容正在抓紧时间编辑中,请耐心等待
崔老师
男,中教高级职称
市优秀教师、骨干教师,数学学科带头人。在教学中注重学生自学能力和数学思维能力的培养,教学成绩突出。

九年级数学上册第3章《对圆的进一步认识》3.2 确定圆的条件(第一课时)

九年级数学上册第3章《对圆的进一步认识》3.1 圆的对称性(复习与巩固)

九年级数学上册第3章《对圆的进一步认识》3.1 圆的对称性(第三课时)

九年级数学上册第3章《对圆的进一步认识》3.1 圆的对称性(第二课时)

九年级数学上册第3章《对圆的进一步认识》3.1 圆的对称性(第一课时)

九年级数学上册第2章《解直角三角形》(综合复习第二课时)

九年级数学上册第2章《解直角三角形》(综合复习第一课时)

九年级数学上册第2章《解直角三角形》2.5 解直角三角形的应用(复习与巩固)

九年级数学上册第2章《解直角三角形》2.5 解直角三角形的应用(第三课时)
 正在播放
正在播放
九年级数学上册第2章《解直角三角形》2.5 解直角三角形的应用(第二课时)
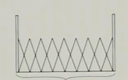
九年级数学上册第2章《解直角三角形》2.5 解直角三角形的应用(第一课时)

九年级数学上册第2章《解直角三角形》2.4 解直角三角形(第二课时)

九年级数学上册第2章《解直角三角形》2.4 解直角三角形(第一课时)

九年级数学上册第2章《解直角三角形》2.3 用计算机求锐角三角比(第二课时)

九年级数学上册第2章《解直角三角形》2.3 用计算机求锐角三角比(第一课时)

九年级数学上册第2章《解直角三角形》2.2 30°、45°、60°角的三角比

九年级数学上册第2章《解直角三角形》2.1 锐角三角比

九年级数学上册第1章《图形的相似》(综合复习第二课时)

九年级数学上册第1章《图形的相似》(综合复习第一课时)

九年级数学上册第1章《图形的相似》1.4 图形的位似(复习与巩固)
评论
点此登录 后即可畅所欲言