课程内容
九年级数学上册第2章《解直角三角形》2.4 解直角三角形(第一课时)
第二章 解直角三角形
2.4 解直角三角形
第一课时
观察与思考
(1)在Rt△ABC中(图2-8),∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.除直角C已知外,
你会用含有字母的等式把其他5个元素之间的关系表示出来吗?与同学交流.
①角之间的关系:∠A+∠B=90°;
②边之间的关系:a²+b²=c²;
③角与边之间的关系:sinA=a/c,cosA=b/c,tanA=a/b.
(2)观察上面的三组等式,你发现在直角三角形中,除直角以外,至少知道几个元素就可以求出其他的未知元素?
例1
在Rt△ABC中,已知∠C=90°,a=17.5,c=62.5.解这个直角三角形.
解
∵a²+b²=c²,∴b=
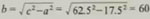
由sinA=a/c=17.5/62.5=0.25,得∠A=16°15´37".
∴∠B=90°-∠A=90°-16°15´37"=73°44´23".
想一想,例1还有其他解法吗?如果已知直角三角形的两条直角边,如何解直角三角形呢?与同学交流.
例2
在Rt△ABC中,已知∠C=90°,c=128,∠B=52°.解这个直角三角形(边长精确到0.01).
解
在Rt△ABC中,已知∠C=90°,∠B=52°得
∠A=90°-∠B=90°-52°=38°.
由sinB=b/c,得b=c·sinB=128·sin52°≈100.87;
由cosB=a/c,得
a=c·cosB=128·cos52°≈78.80.
想一想,如果已知直角三角形的一条直角边和一个锐角,如何解直角三角形呢?
由例1和例2,你能总结一下已知直角三角形的两边或已知直角三角形的一边及一个锐角解直角三角形的思路吗?
复习与巩固
1.在Rt△ABC中,∠C=90°,根据下列条件,解直角三角形:
(1)
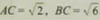
;(2)∠A=22.5°,b=12.
2.在Rt△ABC中,∠C=90°.
(1)已知c=39,b=36,求a和∠B(精确到1´);
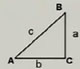
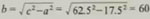
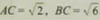 ;(2)∠A=22.5°,b=12.
;(2)∠A=22.5°,b=12.
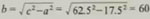
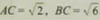 ;(2)∠A=22.5°,b=12.
;(2)∠A=22.5°,b=12.