课程内容
九年级数学上册第2章《解直角三角形》2.2 30°、45°、60°角的三角比
第二章 解直角三角形
2.2 30°、45°、60°角的三角比
实验与探究
(1)要想求出45°角的正弦、余弦和正切的值,可以考察45°锐角的直角三角形。
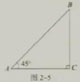
作Rt△ABC,使∠C=90°,∠A=45°(图2-5).设a=1,那么b=1.
由勾股定理,
于是
tan45°=a/b=1/1=1.
(2)怎样才能求出30°角的各三角比的值呢?
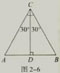
取两个含30°角的大小相等的三角尺,按图2-6的方式拼在一起,得到的△ABC是怎样的三角形?为什么?
因为∠A=∠B=60°,所以△ABC是等边三角形,且CD是AB边上的高,AD=BD.
在Rt△ADC中,∠ADC=90°,∠ACD=30°.
设AC=1,那么AD=1/2AB=1/2,
于是
sin30°=AD/AC=1/2÷1=1/2;
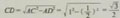
(3)利用图2-6,你会求出60°角的正弦、余弦和正切的值吗?与同学交流。
观察与思考
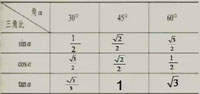
把30°,45°,60°角的正弦、余弦、正切的值填入下表:
从填写的表格中,你发现了哪些规律?与同学交流。
例1 求下列各式的值:
(1)sin30°·cos45°;
(2)tan45°-cos60°.
解
(1)sin30°·cos45°=

(2)tan45°-cos60°=1-1/2=1/2.
例2 在Rt△ABC中,已知sinA=

,求锐角A的度数.
因为A是锐角,并且sinA=,由于sin60°=,所以∠A=60°.
挑战自我
如图2-7,作等腰三角形ABC,延长边CA到D使AD=AB.连接DB。你能利用图求出22.5°角的正切的值吗?试一试。
练习
1.求下列各式的值:
(1)sin30°+cos60°; (2)tan30°·tan60°;
(2)2sin60°-tan30°; (4)sin45°·cos45°+tan45°.
2.已知α是锐角,当α=____时,tanα=1,这时cosα=_____.
复习与巩固
1.求出下列各式的值;
(1)sin60°-3tan30°+2cos45°;
(2)tan60°+9tan30°-1/2tan45°+sin30°;
(3)cos60°+

sin45°+tan30°·cos30°;
(4)sin60°·cos60°+sin45°·cos45°-sin30°·cos30°.
2.求下列各式中锐角A的值;
(1)cosA=1/2;
(2)cosA=

;
(3)tanA=

;
(4)sinA=1/2.
3.已知α是锐角,当α=___时,cosα=

,这时tanα=___.
4.在Rt△ABC中,∠C=90°,
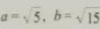
求∠A。∠B的度数.
探索与创新
5.利用类似于本节“挑战自我”中的方法,构造一个图形,然后利用这个图形求15°及75°角的正切的值.

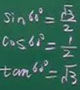


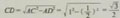


 ,求锐角A的度数.
,求锐角A的度数.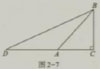
 sin45°+tan30°·cos30°;
sin45°+tan30°·cos30°; ;
; ; (4)sinA=1/2.
; (4)sinA=1/2. ,这时tanα=___.
,这时tanα=___.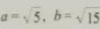 求∠A。∠B的度数.
求∠A。∠B的度数.
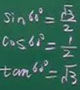



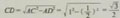




 ,求锐角A的度数.
,求锐角A的度数.
 sin45°+tan30°·cos30°;
sin45°+tan30°·cos30°; ;
; ; (4)sinA=1/2.
; (4)sinA=1/2. ,这时tanα=___.
,这时tanα=___.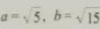 求∠A。∠B的度数.
求∠A。∠B的度数.