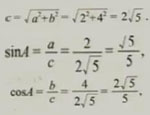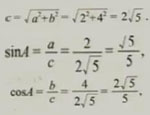课程内容
九年级数学上册第2章《解直角三角形》2.1 锐角三角比
第二章 解直角三角形
2.1 锐角三角比
实验与探究
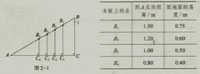
(1)有一块长2.00m的平滑木板AB,小亮将它的一端B架高1m,另一端A放在平地上(图2-1),在木板上分别
取点B₁,B₂,B₃,B4,分别量得它们到A点的距离,AB₁,AB₂,AB₃,AB4,以及它们距地面的高度B₁C₁,B₂C₂,B₃C₃,B4C4,数
据如下表所示:
利用上述数据,分别计算比值BC/AB,B₁C₁/AB₁,B₂C₂/AB₂,B₃C₃/AB₃,B4C4/AB4,你有什么发现?
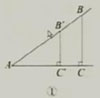
(2)如图2-2①,∠A是锐角,在∠A的一边上任意取两个点B,B´,经过这两个点分别向∠A的另一边作垂线,
垂足分别为点C,C´,由(1)你猜测比值BC/AB与B´C´/AB´相等吗?能证明你的结论是正确的吗?
(3)如果比值B´C´/AB´=k.由(2)你发现当锐角A大小确定后,k的大小与点B´在AB边上的位置有关吗?
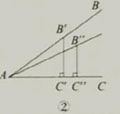
(4)如图2-2②,以A为端点,在锐角A的内部(或外部)作一条射线,在这条射线上取点B",使AB"=AB´,这
样又得到了一个锐角∠B"AC。过B"作B"C"⊥AC,垂足为C"点。比值B"C"/AB"与K相等吗?为什么?由此你得到
怎样的推论?
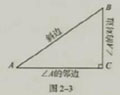
由上面的探索,我们可以利用Rt△ABC(图2-3)把比值k记作∠A的对边/斜边,当锐角A的大小确定后,不论
以∠A为锐角的直角三角形的大小如何,这个比值也就随之确定。
我们把锐角A的对边与斜边的比叫做正弦(sine),记作sinA,即sinA=∠A的对边/斜边.
类似地,当锐角A的大小确定后,比值∠A的邻边/斜边和比值∠A的对边/∠A的邻边也随之确定。我们把锐角A
的邻边与斜边的比叫做余弦(cosine),记作cosA,即cosA=∠A的邻边/斜边.
把锐角A的对边与邻边的比叫做∠A的正切(tangent),记作tanA,即
tanA=∠A的对边/∠A的邻边
锐角A的正弦、余弦、正切统称锐角A的三角比(trigonometric ratio.)
在图2-3中,把∠A的对边记作a,∠B的对边记作b,∠C的对边记作c.
小资料
在Rt△ABC中,∠C=90°,如果用a,b分别表示∠A的对边和邻边,c表示斜边。那么sinA=a/c,cosA=b/c,
tanA=a/b.
sinA,cosA,tanA分别是一个完整的记号.当角只用一个大写字母或小写字母表示时,习惯上在记号中省去角
的符号“∠”,不能理解成sin·A,cos·A,tan·A.
例1
如图2-4,在Rt△ABC中,∠C=90°.
∠C=90°.a=2.b=4.求∠A的正弦、余弦、正切的值.
解 在Rt△ABC中,∠C=90°.
∵a=2,b=4,所以
tanA=a/b=2/4=1/2.
练习
1.如果Rt△ABC∽Rt△A´B´C´,∠C=∠C´=90°,sinA等于sinA´吗?为什么?cosA与cosA´吗?
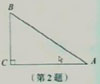
2.如图,在Rt△ABC中,∠C=90°,c=3,a=2,求∠A的正弦、余弦、正切的值.
复习与巩固
1.在Rt△ABC中,∠C=90°,根据下列条件求出∠A和∠B的正弦、余弦的值:
2.在Rt△ABC中,∠C=90°,AB=2AC,求cosB和tanA的值.
3.在Rt△ABC中,∠C=90°,BC=8,sinA=4/5,求cosA和tanB的值.
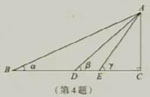
4.如图,在Rt△ABC中,∠C=90°,AC=4,点D,E在BC上,BD=5,DE=2,EC=3.
设∠ABC=α,∠ADC=β,∠AEC=y,求tanα,cosβ,siny的值.