课程内容
九年级数学上册第1章《图形的相似》1.2 怎样判定三角形相似(第四课时)
第一章 图形的相似
1.2 怎样判定三角形相似
第四课时
观察与思考
(1)我们知道,三边分别相等的两个三角形全等,如果把条件“三边相等”改为“三条边成比例”,这两个三角形相似吗?
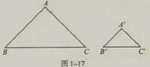
(2)如图1-17,把△ABC的三边按一定的比例缩小(或放大)后得到△A´B´C´,这时两个三角形三边之间的
关系满足A´B´/AB=A´C´/AC=B´C´/BC.观察所得到的△A´B´C´,它与△ABC相似吗?怎样才能证明你的结论呢?
证明
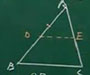
如图1-18,在AB(或它的延长线)上截取AD=A´B´,过点D作DE//BC,交AC于点E.于是AD/AB=AE/AC=DE/BC(基本事实9推论).①
∵A´B´/AB=A´C´/AC=B´C´/BC,②
AD=A´B´
∴AD/AB=A´B´/AB.
比较①②可得,AE/AC=A´C´/AC,DE/BC=B´C´/BC.
∴AE=A´C´,DE=B´C´ ∴△ADE≌△A´B´C´(SSS).
∴∠A=∠A´
∴△ABC∽△A´B´C´(相似三角形的判定定理2).
于是,便得到
相似三角形的判定定理3 三边成比例的两个三角形相似。
例3
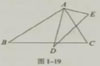
如图1-19,已知AB/AD=BC/DE=AC/AE,不另外添加字母,写出图中相等的角,并说明理由.
解:在△ABC于△ADE中,
∵AB/AD=BC/DE=AC/AE,
∴△ABC∽△ADE(相似三角形的判定定理2).
∴∠BAC=∠DAE,∠ABC=∠ADE,∠C=∠E.
由∠BAC=∠DAE还可推出∠BAD=∠CAE.
总结:利用相似三角形可以证明角的相等。
挑战自我
(1)如果两个三角形的三条边的比都是3:4:5,这两个三角形相似吗?
(2)在什么条件下两个等腰三角形相似?在什么条件下两个直角三角形相似?
练习
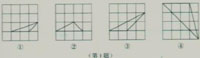
1.在如图所示的正方形网格中,各画有一个格点三角形,找出其中的相似三角形。
2.已知三角形三边的长分别为4,5,6,画出与它相似的另一个三角形,使它的一条边长为2.你能画出几种符合
要求的三角形?与同学交流。