Beginning of dialog window. Escape will cancel and close the window.
End of dialog window.

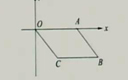
 ,
, 被平行直线
被平行直线 ,
,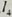 所截,交点分别为A,B,C,D.过线段AB的中点E,作直线
所截,交点分别为A,B,C,D.过线段AB的中点E,作直线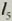 ∥
∥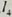 ,
,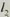 与点E.F是线段DC的中点吗?如果是,证明你的结论。
与点E.F是线段DC的中点吗?如果是,证明你的结论。 ,
,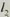 被三条平行直线
被三条平行直线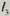 ,
,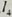 ,
,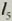 所截,如果在
所截,如果在 上截得的两条线段的比等于1:1,那么在
上截得的两条线段的比等于1:1,那么在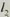 上截得的两条线段的比也等于1:1,也就是说这时截得的四条线段成比例。
上截得的两条线段的比也等于1:1,也就是说这时截得的四条线段成比例。 被
被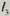 ,
,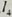 ,
,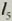 所截得的线段不相等,上面的结论能进一步推广吗?
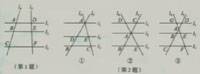
所截得的线段不相等,上面的结论能进一步推广吗?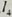 ∥
∥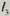 交于点Q(图1-5①),此时对应线段AP,PB,DQ,QC成比
交于点Q(图1-5①),此时对应线段AP,PB,DQ,QC成比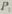 ,过点
,过点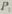 作直线
作直线 ∥
∥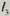 ,交
,交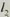 于点Q3(图1-5②),你发现,被平行线
于点Q3(图1-5②),你发现,被平行线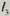 ,
, ,
,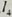 截得的对应线段
截得的对应线段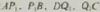 成比例吗?(图1-5②)
成比例吗?(图1-5②)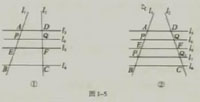
 ,
, 被一组平行直线
被一组平行直线 ,
,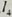 ,
,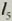 所截,交点分别是A,B,C,D,E,F(图1-6)。都有
所截,交点分别是A,B,C,D,E,F(图1-6)。都有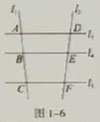
 //
//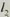 //
//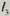 ,AB=3cm,BC=5cm,DE=24cm,求DF的长。
,AB=3cm,BC=5cm,DE=24cm,求DF的长。 //
//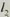 //
//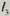 ,直线
,直线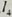 ,
,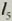 分别与
分别与 ,
,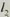 ,
,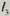 ,相交,直线
,相交,直线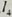 与
与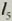 相交于点A。
相交于点A。