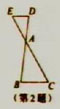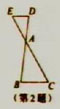课程内容
九年级数学上册第1章《图形的相似》1.1 相似多边形
第一章 图形的相似
1.1 相似多边形
交流与发现
五星红旗是中华人民共和国的国旗,国旗上的左上角有五颗五角星(图1-1),这五颗五角星的形状相同吗?
大小相等吗?
在现实生活中,你还见过形状相同但大小未必相等的图形吗?
形状相同的平面图形叫做相似形(similar figures)
全等行与相似性有什么关系?
观察与思考
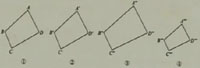
小莹在电脑上任意画出一个四边形ABCD(图1-2①),并将它按原大复制下来,得到四边形A´B´C´D´(图-1-2
②)然后将四边形ABCD各角的大小保持不变,将它的各边同时放大5/4倍,得到四边形A"B"C"D"(图1-2③)
,再将四边形ABCD各角的大小保持不变,将它的各边同时缩小2/3,得到四边形A"´B"´C"´D"´(图1-2④)把
这四个四边形打印在同一张纸上(图1-2)。
(1)观察得到的四个四边形,你发现它们的形状和大小有什么特征?它们是相似形吗?
(2)观察1-2①和③,在四边形ABCD与四边形A"B"C"D"中,∠A与∠A",∠B与∠B",∠C与∠C",∠D与∠D"
之间分别具有怎样的数量关系?相应的各边的比AB/A"B",BC/B"C",CD/C"D",DA/D"A"之间有怎样的关系?
(3)观察图1-2①和④,四边形ABCD与四边形A"´B"´C"´D"´相应的各角及相应的各边具有怎样的数量关系?
图③和图④呢?
由上面的探究过程,我们发现:把四边形ABCD复制,放大或缩小后,所得到的四边形与原来的四边形相似,
它们的各个角对应相等,各边对应成比例。反过来,如果一个四边形与四边形ABCD的各角对应相等,并且各
边对应成比例,那么这个四边形与四边形ABCD形状相同,也就是说,这个四边形与四边形ABCD相似,由此,
可以给出相似多边形的定义:
两个边数相同的多边形,如果一个多边形的各个角与另一个多边形的各个角对应相等,各边对应成比例,那
么这两个多边形叫做相似多边形(similar polygons)。
如图1-2,四边形ABCD与四边形A"B"C"D"相似,记作四边形ABCD∽四边形A"B"C"D",符号“∽”读作“相似于
”,与三角形全等的表示方法一样,在记两个多边形相似时,要把表示对应顶点的字母写在对应的位置上。
相似多边形的对应边的比叫做相似比(similarity ratio)。例如,在图1-2中,四边形A"B"C"D"与四边形
ABCD的形似比为5/4,或说成5:4,四边形A"´B"´C"´D"´与四边形ABCD的相似比为2/3,当两个多边形相等时,
其相似比为1;反之,如果两个相似多边形的形似比为1,那么这两个多边形全等。
例1
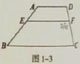
如图1-3,已知四边形AEFD∽四边形EBCF。
(1)写出它们相等的角及对应边的比例式;
(2)若AD=3,EF=4,求BC的长。
解:(1)在四边形AEFD和四边形EBCF中,
∵四边形AEFD∽四边形EBCF,
∴∠A=∠BEF,∠AEF=∠B,∠DFE=∠C,∠D=∠EFC.并且AE/EB=EF/BC=DF/FC=AD/EF.
(2)∵AD=3,EF=4,代入EF/BC=AD/EF得,4/BC=3/4.
解得BC=16/3.
挑战自我
由两个多边形的各个角分别相等,能判断它们相似吗?由两个多边形的边对应成比例,能判断它们相似吗?
如果不能,请分别举出反例;如果能,说明你的理由。
练习
1.三角形与四边形能相似吗?等边三角形与直角三角形能相似吗?为什么?
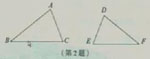
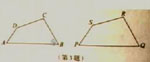
2.如图,△ABC∽△DFE,点A与D,点B与点F是对应顶点,请写出它们的对应角、对应边以及对应边之间的比例式。
习题1.1
复习与巩固
1.如果五边形ABCDE∽五边形A´B´C´D´E´,且五边形ABCDE与A´B´C´D´E´的相似比为k1,五边形A´B´C´D´E´与
ABCDE的相似比为k2,那么k1与k2满足怎样的数量关系?
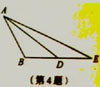
2.如图,已知△DEA∽△BCA,
(1)BC//DE吗?为什么?
(2)如果BC=3.6,ED=2.4,AE=5,求AC的长。
3.如图,四边形ABCD∽四边形PQRS,BC=8,QR=10,PS=6,∠B=64°,求;
(1)∠Q的度数;
(2)AD的长;
(3)求四边形ABCD与四边形PQRS的相似比。
拓展与延伸
4.如图,△BEA∽△SAD,写出图中所有相等的角和成比例线段的比例式。