
此内容正在抓紧时间编辑中,请耐心等待
王老师
女,小教高级职称
数学功底扎实,逻辑思维严密。热爱教育,有多年教学经验,讲课风趣幽默,亲和力强;条理清晰,重点突出。

此内容正在抓紧时间编辑中,请耐心等待
王老师
女,小教高级职称
数学功底扎实,逻辑思维严密。热爱教育,有多年教学经验,讲课风趣幽默,亲和力强;条理清晰,重点突出。

五年级数学下册总复习(一)

五年级数学下册第七章《包装盒——长方体和正方体》长方体和正方体整理和复习(二)

五年级数学下册第七章《包装盒——长方体和正方体》不规则物体体积

五年级数学下册第七章《包装盒——长方体和正方体》长方体和正方体体积

五年级数学下册第七章《包装盒——长方体和正方体》容积和容积单位
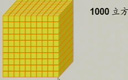
五年级数学下册第七章《包装盒——长方体和正方体》体积单位间的进率

五年级数学下册第七章《包装盒——长方体和正方体》体积和体积单位

五年级数学下册第五章《关注环境——分数加减法(二)》分数加减法整理复习(二)

五年级数学下册第七章《包装盒——长方体和正方体》长方体和正方体整理和复习(一)
 正在播放
正在播放
五年级数学下册第七章《包装盒——长方体和正方体》长方体表面积和体积的比较

五年级数学下册第七章《包装盒——长方体和正方体》长方体和正方体体积练习课

五年级数学下册第七章《包装盒——长方体和正方体》容积的计算方法

五年级数学下册第七章《包装盒——长方体和正方体》长方体和正方体的表面积练习课

五年级数学下册第七章《包装盒——长方体和正方体》正方体的表面积
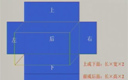
五年级数学下册第七章《包装盒——长方体和正方体》长方体的表面积

五年级数学下册第七章《包装盒——长方体和正方体》长方体的认识

五年级数学下册第五章《关注环境——分数加减法(二)》异分母分数连加连减

五年级数学下册第五章《关注环境——分数加减法(二)》异分母分数加减法练习课

五年级数学下册第五章《关注环境——分数加减法(二)》异分母分数加减法
五年级数学下册第五章《关注环境——分数加减法(二)》通分练习课
评论
点此登录 后即可畅所欲言