课程内容
第28章《锐角三角函数》28.2 解直角三角形(2)
仰角,俯角在解直角三角形中的应用
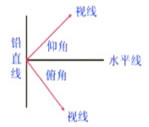
仰角和俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角。
当堂反馈
如图,在离铁塔BE120m的A处,用测角仪测量塔顶的仰角为30°,已知测角仪高AD=1.5m,则塔高BE=___________(根号保留)。
例题
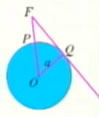
例3:2003年10月15日“神舟”5号载人航天飞船发射成功。当飞船完成变轨后,就在离地球表面350km的圆形轨道上运行。如图,当飞船运行到地球表面上P点的正上方时,从飞船上最远能直接看到地球上的点在什么位置?这样的最远点与P点的距离是多少?(地球半径为6400km,结果精确到0.1km)
解:在图中,FQ是⊙O的切线,△FOQ是直角三角形。
∵cosα=OQ/OF=6400/(6400+350)≈0.95
∴α≈18°
∴PQ的长为(18π/180)×6400≈3.14×640≈2009.6
当飞船在P点正上方时,从飞船观测地球时的最远点距离P点约2009.6km。
例4:热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m)
解:由题意可得α=30°,β=60°,AD=120
∵tanα=BD/AD,tanβ=CD/AD
∴BD=AD·tanα=120×tan30°
=120×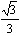 =40
=40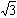
CD=AD·tanβ=120×tan60°
=120×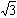 =120
=120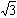
∴BC=BD+CD=40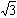 +120
+120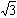
=160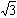 ≈277.1
≈277.1
答:这栋楼高约为277.1m。
合作与探究
如图,直升飞机在跨江大桥AB的上方P点处,此时飞机离地面的高度PO=450米,且A、B、O三点在一条直线上,测得大桥两端的俯角分别为α=30°,β=45°,求大桥的长AB。
变题1:如图,直升飞机在长400米的跨江大桥AB的上方P点处,且A、B、O三点在一条直线上,在大桥的两端测得飞机的仰角分别为30°和45°,求飞机的高度PO。
例2:如图,直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机的高度PO。
变式2:如图,直升飞机在高为200米的大楼AB左侧P点处,测得大楼的顶部仰角为45°,测得大楼底部俯角为30°,求飞机与大楼之间的水平距离。
思想与方法
解题思想与方法小结:
1、数形结合思想。
2、方程思想。
3、转化(化归)思想。
方法:把数学问题转化成解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,构造出直角三角形。
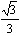 =40
=40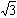
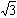 =120
=120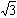
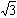 +120
+120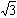
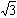 ≈277.1
≈277.1

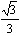 =40
=40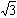
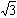 =120
=120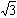
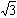 +120
+120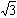
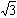 ≈277.1
≈277.1