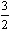 。
。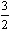 ,4×
,4×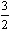 ),即(-3,6)。类似地,可以确定其他顶点的坐标。
),即(-3,6)。类似地,可以确定其他顶点的坐标。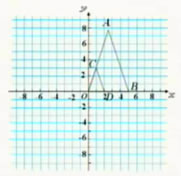
此内容正在抓紧时间编辑中,请耐心等待
刘老师
女,中教中级职称
从教20年,市优秀青年人才、优秀教师,曾在全省、全国青年教师课堂教学大赛中获奖。
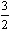 。
。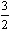 ,4×
,4×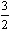 ),即(-3,6)。类似地,可以确定其他顶点的坐标。
),即(-3,6)。类似地,可以确定其他顶点的坐标。
此内容正在抓紧时间编辑中,请耐心等待
刘老师
女,中教中级职称
从教20年,市优秀青年人才、优秀教师,曾在全省、全国青年教师课堂教学大赛中获奖。

九年级数学下册第29章《投影与视图》29.2 三视图(第1课时)

九年级数学下册第29章《投影与视图》29.1 投影(第3课时)

九年级数学下册第29章《投影与视图》29.2 三视图(第4课时)

九年级数学下册第29章《投影与视图》29.2 三视图(第3课时)

九年级数学下册第29章《投影与视图》29.2 三视图(第2课时)

九年级数学下册第29章《投影与视图》29.1 投影(2)(旧版)

九年级数学下册第29章《投影与视图》29.1 投影(1)(旧版)

九年级数学下册第28章《锐角三角函数》28.2 解直角三角形(2)

九年级数学下册第28章《锐角三角函数》28.2 解直角三角形(1)
 正在播放
正在播放
九年级数学下册第27章《相似》27.3 位似(2)

九年级数学下册第29章《投影与视图》29.2 三视图(2)(旧版)

九年级数学下册第29章《投影与视图》29.2 三视图(1)(旧版)

九年级数学下册第28章《锐角三角函数》28.2 解直角三角形(4)

九年级数学下册第28章《锐角三角函数》28.2 解直角三角形(3)

九年级数学下册第28章《锐角三角函数》28.1 锐角三角函数(3)

九年级数学下册第28章《锐角三角函数》28.1 锐角三角函数(2)

九年级数学下册第28章《锐角三角函数》28.1 锐角三角函数(1)

九年级数学下册第27章《相似》27.3 位似(1)

九年级数学下册第27章《相似》27.2.3 相似三角形应用举例

九年级数学下册第27章《相似》27.2.2 相似三角形的性质
评论
点此登录 后即可畅所欲言
[四川省德阳市] 还行

180****1036
2017-11-05 16:16:13
[河北省邢台市] Good

155****9058
2017-07-25 17:25:01
[甘肃省兰州市] Good!Good!真的好!

0930666735
2017-02-17 13:29:51