课程内容：
《算法的概念》
复习：
问题1：求二元一次方程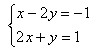
的解。
问题2：用加减消元法解二元一次方程组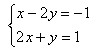
的具体步骤是什么？
问题3：写出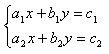
（a1b2-a2b1=0）的求解步骤。
问题4：到底什么是算法？
在数学中，算法通常是指按照一定规则解决某一类问题的明确和有限的步骤。
现在，算法通常可以编成计算机程序，让计算机执行并解决问题。
例题：变式1：设计一个算法，判断35是否为质数。
变式2：设计一个算法，判断1997是否为质数。
思考：一般地，判断任意一个大于2的整数是否为质数的算法步骤如何设计？
例2.用二分法设计一个求方程x2-2=0（x＞0）的近似解得算法。
练习1：有人对哥德巴赫猜想“任何大于4的偶数都能写成两个质数之和”设计了如下操作步骤：
第一步，检验6=3+3
第二步，检验8=3+5
第三步，检验10=5+5
……
利用计算机无穷地进行下去！请问：这是一个算法吗？
练习2：任意给定一个大于1的正整数n，设计一个算法求出n的所有因数。
本节重点：
1.体会算法的思想，理解算法的含义，了解算法的特征，能用自然语言描述算法。
2.培养学习的逻辑思维能力和问题解决的条理性。
本节难点：
根据实例抽象概括算法的概念和特点；依据概念设计算法。
易考点：
通过分析具体问题过程与步骤，建立算法的概念，了解算法的含义，体会算法的思想，能用自然语言描述解决具体问题的算法。
常老师
女，中教中级职称
从教30年，数学教研组长，省级“先进教育工作者”、优秀教师，市级骨干教师、“教学标兵”。
