课程内容
第26章《反比例函数》26.1.2 反比例函数的图象与性质(1)
知识回顾
1、什么是反比例函数?
一般地,形如y=k/x(k为常数,k≠0)的函数叫做反比例函数。
2、反比例函数的定义中需要注意什么?
(1)k是非零常数。
(2)xy=k。
知识回顾
(1)任意写一个在第二象限的点的坐标:________。
(2)直线y=-x+3经过第_____象限。
(3)已知矩形的面积为6,则它的长y与宽x之间的函数关系式为________,y是x的_____函数。
(4)若函数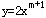 是反比例函数,则m=________。
是反比例函数,则m=________。
(5)反比例函数y=4/x经过点(1,___)。
新课导入
1、一次函数的图象与性质是怎样的?
2、二次函数的图象与性质是怎样的?
3、如何画函数的图象?
描点法:列表→描点→连线
想一想:反比例函数的图象与性质又是怎样的呢?这就是我们从这节课开始探究的内容。
学习目标
1、进一步熟悉作函数图象的步骤,会画反比例函数的图象;
2、体会函数的三种表示方法的相互转换,逐步提高从函数图象获取信息的能力;
3、探索并掌握反比例函数的主要性质。
反比例函数图象的画法
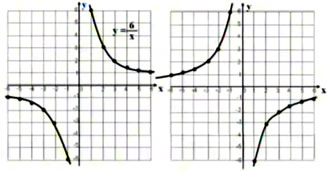
画出反比例函数y=6/x和y=-6/x的函数图象。
| x |
… |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
1 |
2 |
3 |
4 |
5 |
6 |
… |
| y=6/x |
… |
-1 |
-1.2 |
-1.5 |
-2 |
-3 |
-6 |
6 |
3 |
2 |
1.5 |
1.2 |
1 |
… |
| y=-6/x |
… |
1 |
1.2 |
1.5 |
2 |
3 |
6 |
-6 |
-3 |
-2 |
-1.5 |
-1.2 |
-1 |
… |
你认为作反比例函数图象时应注意哪些问题?
1、列表时,在自变量取值范围内取一些值,并计算相应的函数值。选取的自变量的值,既要易于计算,又要便于描点,尽量多取一些数值(取互为相反数的一对一对的数),多描一些点,这样既可以方便连线,又可以使图象精确。
2、描点时,要严格按照表中所列的对应值描点,绝对不能把点的位置描错。
3、连线时,一定要养成按自变量从小到大的顺序依次画线,连线时必须用光滑的曲线连接各点,不能用折线连接。
4、图象是延伸的,注意不要画的有明确端点。
反比例函数的图象是由两支曲线组成的。故称反比例函数的图象为双曲线。
反比例函数的图象在哪两个象限,是由什么决定的?y随x的变化有怎样的变化?
由k的符号决定。
当k>0时,两支曲线分别位于第一、三象限内,y随x的增大而减小;
当k<0时,两支曲线分别位于第二、四象限内,y随x的增大而增大。
归纳:反比例函数的图象和性质
1、反比例函数的图象是双曲线。
2、图象性质见下表:
| y=k/x |
k>0 |
k<0 |
| 图象 |
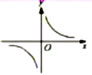 |
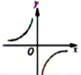 |
| 性质 |
当k>0时,函数图象的两个分支分别在第一、三象限,在每个象限内,y随x的增大而减小 |
当k<0时,函数图象的两个分支分别在第二、四象限,在每个象限内,y随x的增大而增大 |
跟踪练习1
1、函数y=20/x的图象在第________象限,在每一象限内,y随x的增大而______。
2、函数y=-30/x的图象在第________象限,在每一象限内,y随x的增大而______。
3、函数y=π/x,当x>0时,图象在第_____象限,y随x的增大而______。
跟踪练习2
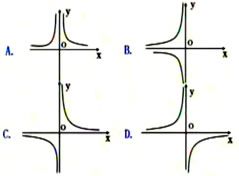
反比例函数y=-5/x的图象大致是( )
跟踪练习3
已知反比例函数y=(4-k)/x。
(1)若函数的图象位于第一、三象限,则k______;
(2)若函数的图象位于第二、四象限,则k______。
跟踪练习4
考察函数y=2/x的图象,当x=-2时,y=______;当x<-2时,y的取值范围是______;当y<-1时,x的取值范围是______。
跟踪练习5
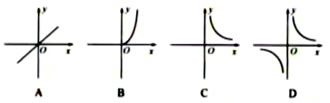
甲乙两地相距100km,一辆汽车从甲地开往乙地,把汽车到达乙地所用的时间y(h)表示为汽车的平均速度x(km/h)的函数,则个函数的图象大致是( )
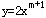 是反比例函数,则m=________。
是反比例函数,则m=________。