课程内容
五年级数学上册第四章《多边形的面积》整理与复习
练习五
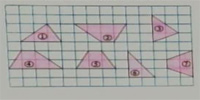
1.下图中每个小方格的边长表示1cm。
(1)说一说,图中哪两个图形的面积相等?
(2)哪两个图形可以拼成平行四边形?与同伴交流。
面积相等的图形:(1)、(3)和(6) (2)和(4) (5)和(7)
能拼成平行四边形的图形:(1)和(3) (2)和(4) (5)和(7)
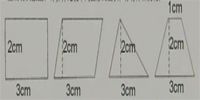
2.量出有关数据,计算并比较下列图形的面积,你有什么发现?
3×2=6(平方厘米) 3×2÷2=3(平方厘米)
3×2=6(平方厘米) (3+1)×2÷2=4(平方厘米)
3.涂色的三角形面积是平行四边形面积的一半吗?说一说你的理由。
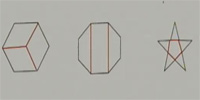
4.下面的图形是由哪些基本图形(长方形、平行四边形、三角形或梯形)组成的?请你动手画一画,并与同伴交流。
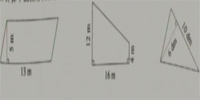
5.计算下面图形的面积。
13×5=65(平方米) (4+12)×16÷2 10×6÷2
=16×16÷2 =60÷2
=256÷2 =30(平方分米)
=128(平方米)
6.如图,一个直角塞纳侥幸的面积是90平方厘米,一条直角边长7.2厘米,另一条直角边长是多少?
90×2÷7.2
=180÷7.2
=25(cm)
答:另一条直角边长25cm。
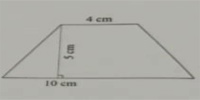
7.(1)如图,梯形的面积是多少?
(2)如果把这个梯形的上底增加1cm,下底减少1cm,得到的新梯形和原梯形的面积之间有什么关系?
(3)如果梯形的上底增加2cm,下底减少2cm呢?
(4)你发现了什么?尝试说明理由。
(1)(4+10)×5÷2=35(平方厘米)
(2)(4+1+10-1)×5÷2=35(平方厘米) 面积不变。
(3)(4+2+10-2)×5÷2=35(平方厘米) 面积不变。
(4)梯形上底增加几厘米,下底减少相同的长度,上、下底的和不变,梯形的高不变,因此梯形的面积也不变。
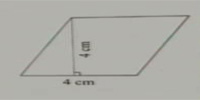
8.(1)如图,平行四边形的面积是多少?
(2)如果平行四边形的高增加1cm,底减少1cm,得到的新平行四边形和原平行四边形的面积之间有什么关系?
(3)如果平行四边形的高增加2cm,底减少2cm呢?
(4)你发现了什么?举例验证你的发现。
(1)4×4=16(平方厘米)
(2)(4+1)×(4-1)=15(平方厘米) 面积减少
(3)(4+2)×(4-2)=12(平方厘米) 面积减少