课程内容

《独立性检验的基本思想及其初步应用》
对于性别变量，其取值为男和女两种，这种变量的不同“值”表示个体所属的不同类别，你这类变量称为分类变量。在现实生活中，分类变量是大量存在的，例如是否吸烟，宗教信仰、国籍，等等。
在日常生活中，我们常常关心两个分类变量之间量来有关系，例如，吸烟与肺癌与吸烟是否有关系？性别对于是否喜欢数学课程有影响？等等。
探究：为调查吸烟是否对肺癌有影响，某肿瘤研究所随机地调查了9965人，得到如下结果（单位：人）
表1-7吸烟与患肺癌列联表

	不患肺癌	患肺癌	总计
不吸烟	7775	42	7817
吸烟	2099	49	2148
总计	9874	91	9965

那么吸烟是否对肺癌有影响？
像表1-7这样列出的两个分类变量的频数表，称为列联表，由吸烟情况和患肺癌情况的列联表可以粗略估计出：在不吸烟者中，有0.54%患有肺癌；在吸烟者中，有2.28%患有肺癌，因此，直观上可以得出结论；吸烟者和不吸烟者患肺癌可能存在差异。
与表格相比，三维柱形图和二维条形图能更直观的=地反映出相关数据的总体状况。


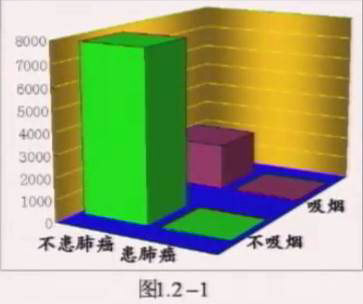
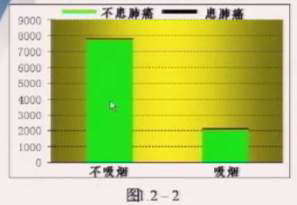
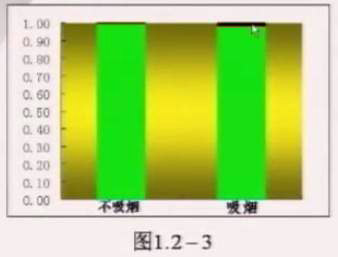
图1.2-1是列联表的三维柱形图，从中能清晰地看出各个频数的相对大小。
作三维柱形图要注意选择恰当的视角，以使每个柱体都能看到。
图1.2-2是叠在一起的二维条形图，其中绿色条高表示不患肺癌的人数，黒色条高表示患肺癌的人数，从图中可以看出，吸烟者中患肺癌的比例高于不吸烟者中患肺癌的比例。
为了更清晰地表达这个特征，我们还可以用如下的等高条形图表示两个情况下患肺癌的比例，如图1.2-3所示，在等高条形图中，绿色的条高表示不患肺癌的百分比；黒色的条高表示患者肺癌的百分比。
上面我们通过分析数据和图形，得到的直观印象是吸烟和患肺癌有关，那么事实是否真的如此呢？或者说我们能够以多大的把握认为“吸烟与患肺癌有关”呢？
为了回答上述问题我们先假设
H_o：吸烟与患肺癌没有关系
用A来表示不吸烟，B表示不患肺癌，则“吸烟与患肺癌没有关系”等价于“吸烟与患肺癌独立”即H_o等价于P=（AB）=P（A）P（B）
把表1-7中的数字用字母代替，得到如下用字母表示的列联表

	不患肺癌	患肺癌	总计
不吸烟	a	b	a+b
吸烟	c	d	c+d
总计	a+c	b+d	a+b+c+d

a/n≈（a+b）/n×（a+c）/n,其中n=a+b+c+d各样本容量，即（a+b+c+d）a≈（a+b）（a+c）,即ad≈bc。因此∣ad-bc∣越小，说明吸烟与患肺癌之间关系越弱；∣ad-bc∣越大，说明吸烟与串肺癌之间关系越强。
为了使不同样本容量的数据有统一的评判标准，基于上面的分析，我们构造一个随机变量
K2=n（ad-bc）²/（a+b）（c+d）（a+c）（b+d）(1)
其中n=a+b+c+d为样本容量
若HO成立，即“吸烟与肺癌者没有关系”，则K2应该很小现在，根据表1.7中的数据，利用公式（1）计算得K2的观测值为
k=｛9965×（7775×49-42×2099）²｝/｛7817×2148×9848×91｝=56.632
这个值是不是很大呢？
在Ho成立的情况下，统计学家估算出如下概率P（K²≥6.635）≈ 0.01（2）
即在Ho成立的情况下K²的值大于6.635的概率非常小近似于0.01，也就是说，在Ho成立的情况
正下对随机变量K2进行多次观测，观测值超过6.635的频率约为1/100。
在（2）中n越大，近似程度越高，在实际应用中，通常要求a，b，c，d都不小于5。
思考 如果K2≥6.635，就断定HO不成立，这种判定出错的可能性有多大？
现在观测值k≈56.632远远大于6.635，在Ho成立的条件下，由（2）式可知能够出现这样的观测值班的概率不超过0.01，因此，我们有99%的把握认为Ho不成立，即有99%的把握认为“吸烟与肺癌有关系”。
上面这种利用随机变量K2来确定在多大程度上可以认为“两个分类变量有关系”的方法称为两个分类变量的独立性检验。
独立性检验的基本思想类似于反证法，要确认“两个分类变量有关系”这一结论成立的可信程度，首先假设该结论不成立，即假设结论“两个分类变量没有关系”成立，在该假设下构造的随机变量K2应该很小，如果由观测数据计算得到K2的观测值很大，则在一定程度上说明假设不合理，根据随机变量K2的含义，可以通过概率（2）式评价该假设不合理的程度，由实际计算出的k﹥6.635，说明假设不合理的程度为99%，即“两个分类变量有关系”这结论成立的可信程度约为99%。
思考 利用上面的结论，你能从列联表的三维柱形图中看出两个分类变量是否相关系？
一般地，假设两个分类变量X和Y，它们值域分别为｛x₁,x₂｝和｛y₁，y₂｝，其样本频数列联表（称为2×2列联表）为：
表1-9    称为2×2列联表

	y1	y2	总计
x1	a	b	a+b
x2	c	d	c+d
总计	a+c	b+d	a+b+c+d

若要推断的结论为H1：“X与Y有关系”，可以按如下步骤判断结论H₁成立的可能性：
1.通过三维柱形图和二维条形图，可以粗略地判断两个分类变量是否有关，但是这种判断无法精确地结出所得结论的可靠程度。
（1）在三维柱形图中，主要对角线上两个柱形高度的乘积ad与副对角线上的两个想得开高度的乘积bc相差越大H₁成立的可能性越大。
（2）在二维条形图中，可以估计满足条件X =x₁的个体中具有Y=y₁的个体所占的比例a/（a+b)，也可以估计满足条件X=x₂的个体中具体有Y=y¹体所占比例c/（c+d）两个比例的值相差越大，H₁成立的可能性越大。
2.可以利用独立检验来考察两个分类变量是否有关系，并且能较精确地给出这种判断的可靠程度，具体做法是：根据观测数据计算则（1）式给出的检验随机变量K²的值k，其值越大说明“X与Y有关系”成立的可能性越大，当得到的观测数据a，b，c,d都不小于5时，可以通过查阅
下表（1-10）来确定结论“X与Y有关系”的可信程度。
例如
（1）如果k﹥10.828，就有99.9%把握认为“X与Y有关系”；
（2）如果k﹥7.879，就有99.5%把握认为“X与Y有关系”；
（3）如果k﹥6.635，就有99%把握认为“X与Y有关系”；
（4）如果k﹥5.024，就有97.5%把握认为“X与Y有关系”；
（5）如果k﹥3.841，就有95%把握认为“X与Y有关系”；
（6）如果k﹥2.706，就有90%把握认为“X与Y有关系”；
如果k≤2.706，就认为没有充分的证据显示“X与Y有关系”。