课程内容

《正太分布》
知道回顾
1.频率分布直方图与总体密度曲线。
2.总体密度曲线的形状特征。

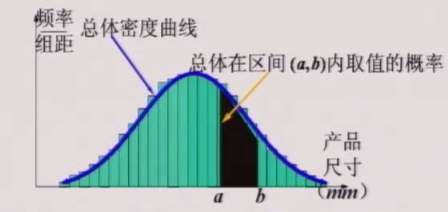
1.正态分布与正态曲线
产品尺寸的总体密度曲线具有“中间高，两头低”的特征，像这种类型的总体密度曲线，一般就是或近似的是以下函数有图像：
f（x）=1/√（2πσ）e^{-（x-μ）2/2σ2}，x∈（-∞，+∞）
式中的实数μ、σ（σ﹥0）是参数，分别表示总体的平均数与标准差，其分布叫做正态分布，由参数μ、σ唯一确定。正态分布常记作N（μ、σ²）。它的图像被称为正态曲线。
2.正态分布的期望与方差
若ξ～N（μ、σ²），则ξ的期望与方差分布为：Eξ=μ，Dξ=σ²
f（x）=1/√（2πσ）e^{-（x-μ）2/2σ2}，x∈（-∞，+∞）
例1：给出下列两个正态总体的函数表达式，请找出其均值μ和标准差σ。
（1）f（x）=1/√（2π）e^-x2/2，x∈（-∞，+∞）
（2）f（x）=1/2√（2π）e^{-（x-2）2/8}，x∈（-∞，+∞）
（3）f（x）=2/√（2π）e^{-2（x+1）2/}，x∈（-∞，+∞）
正态分布
当μ=0，σ=1时，正态总体称为标准正态总体，相应的函数表示是f（x）=1/√（2π）e ^x2/2，x∈R，相应的曲线称为标准正态曲线。
观察以上三条正态曲线，归纳出正态曲线图的性质：

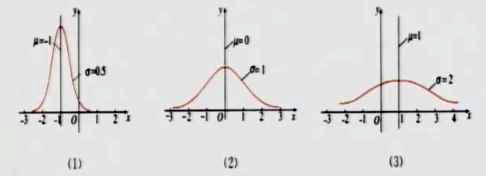
①曲线在x轴的上方，与x轴不相交。
②曲线关于直线x=μ对称，且在x=μ时位于最高点。
③当时x＜μ，曲线上升；当时x﹥μ，曲线下降。并且当曲线向左、右两边无限延伸时，以x轴为渐近线，向它无限靠近。
④当μ一定时，曲线的形状由σ确定。σ越大，曲线越“矮胖”，表示总体的分布越分散；σ越小，曲线越“瘦高”，表示总体的分布越集中。
例2.下列关于正态曲线性质的叙述正确的是（  ）
（1）曲线关于直线x=μ对称，这个曲线只在x轴上方；
（2）曲线关于y轴对称。因为曲线对应的正态密度函数是一个偶函数；
（3）曲线在x=μ时处于最高点，由这一点向左右两边延伸时，曲线逐渐降低；
（4）曲线的对称轴由μ确定，曲线的形态由σ确定；
（5）σ越大，曲线越“矮胖”，总体分布越分散；σ越小，曲线越“高”。总体分布越集中。
例3.把一个正态曲线a沿着横轴方向向右移动2个单位、得到一个新的曲线b、下列说法不正确的是
（A）曲线b仍然是正态曲线；
（B）曲线a和曲线b的最高点的纵坐标相等；
（C）以曲线a为概率密度曲线的总体的方差比以曲线b为概率密度曲线的总体的方差大2；
（D）懭曲线a为概率密度曲线的总体的期望比以曲线b为概率密度曲线的总体的期望小2。
3σ原则
（1）正态分布在三个特殊区间的概率值
p（μ-σ＜X＜μ+σ）=0.6826
p（μ-2σ＜X＜μ+2σ）=0.9544
p（μ-3σ＜X＜μ+3σ）=0.9974
例4、商场经营的某种包装大米质量服从正态分布N(10、0.1²)。任选一袋这种大米，质量在（9.8、10.2）的概率是多少？
解：要求质量在（9.8、10.2）的概率，需要转化为（μ-2σ，μ+2σ）的形式。
p（10-2×0.1＜X＜10+2×0.1）=0.9544
思考题：正态总体N（0.1）的概率密度函数是：
f（x）=1/√（2πσ）e^{-（x-μ）2/2σ2}
（1）求证：f（x）是偶函数；
（2）求f（x）的最大值；
（3）求f（x）的单调区间。