《空间向量的正交分解及其坐标表示》
复习引入
在平面直角坐标第内,分别取与x轴、y轴方向相同的两个单位向量(→,i)、(→,j)为基底,对于任意一个向量(→,a),由平面向量基本定理知,有且只有一对实数x、y,使得(→,a)=x(→,i)+x(→,j)我们把(x、y)叫做向量(→,a)的(直角)坐标,记作:(→,a)=(x、y)。
其中x叫做(→,a)在x轴上的坐标,也员(→,a)的第一分量y叫做(→,a)在y轴上的坐标,也叫(→,a)的第二分量;
显然,(→,i)=(1.0),(→,j)=(0.1),(→,0)=(0.0)
A(x1,y1),B(x2,y2)=>(→,AB)=(x2-x1,y2-y1)
(→,a)=(x1,y1),(→,b)=(x2,y2)
(1)两个向量和与差的坐标分别等于这两个向量相应坐标的和与差;
(1)两个向量和与差的坐标分别等于这两个向量相应坐标的和与差;
(→,a)±(→,b)=(x1±y1,x2±y2) (→,a).(→,b)=x1x2+y1y2
(2)实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标;
若 (→,a)=(x,y) ,则λ (→,a )=(
(2)实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标;
若 (→,a)=(x,y) ,则λ (→,a )=(λx,λy)
(3)向量平行的坐标表示:
(3)向量平行的坐标表示:
(→,a)‖ (→,b)的充要条件为:x1,y2-x2,y1=0
(→,a)⊥ (→,b)的充要条件为:x1,y2+x2,y1=0
思考:空间向量的直角坐标运算是否可以视作平面向量坐标运算的推广?
空间直角坐标系
1、单位下正交基底:如果空间的一个基底的三个基向量互相垂直,且长都为1,则这个基底叫做单位正交基底,常用来{(→,a)⊥ (→,b)的充要条件为:x1,y2+x2,y1=0
思考:空间向量的直角坐标运算是否可以视作平面向量坐标运算的推广?
空间直角坐标系
1、单位下正交基底:如果空间的一个基底的三个基向量互相垂直,且长都为1,则这个基底叫做单位正交基底,常用来{
思考:空间向量的直角坐标运算是否可以视作平面向量坐标运算的推广?
空间直角坐标系
1、单位下正交基底:如果空间的一个基底的三个基向量互相垂直,且长都为1,则这个基底叫做单位正交基底,常用来{(→,i)、(→,j)、(→,k)}表示。
2、空间直角坐标系:在空间选定一点O和一个单位正交基底{
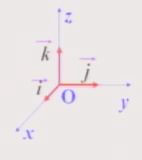
2、空间直角坐标系:在空间选定一点O和一个单位正交基底{(→,i)、(→,j)、(→,k)}。以点O为原点,分别以(→,i)、(→,j)、(→,k)的正方向建立三条数轴:x轴,、y轴、z轴,它们都叫做坐标轴,变样就建立了一个空间直角坐标系O——xyz。
点O叫做原点,向量
点O叫做原点,向量(→,i)、(→,j)、(→,k)都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面。
空间向量的坐标表示


空间向量的坐标表示
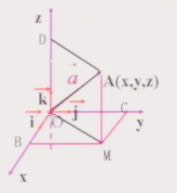
在空间直角坐标系O——xyz中,对空间任一点A,对应一个向量OA,于是存在唯一的有序实数组x,y,z,使OA= (→,xi) (→,yj) (→,zk)
在单位正交基底 (→,i) (→,j) (→,k)中与向量OA对应的有序实数组(x、y、z),叫做点A在此空间直角坐标系中的坐标,记作A(x,y,z),其中x叫做点A的横坐标,y叫做点A的纵坐标,z叫做点A的竖坐标。
单位正交基底,空间直角坐标系,向量的坐标

向量的直角坐标运算
设 (→,a)=(a1,a2,a3,),(→,b)=(b1,b2,b3)则
(→,a)+(→,b)=(a1+b1,a2+b2,a3+b3)
(→,a) - (→,b)=(a1-b1,a2-b2,a3-b3)
λ (→,a)=(λa1,λa2,λa3)(λ∈R)
(→,a).(→,b)=a1b1+a2b2+a3b3
(→,a)∥(→,b)<=>a1=λb1,a1=λb2,a2=λb2,a3=λb3(λ∈R)
(→,a)⊥(→,b)<=>a1 b1+a2b2+a3b3=0
向量的直角坐标运算
①若A(x1,y1,z1),B(x2,y2,z2),则
(→,AB)=(→,OB)-(→,OA)=(x1,y1,z1)-(x2,y2,z2)
=(
=(x2-x1,y2-y1,z2-z1)
注:空间一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标。
②M=(x,y,z),若M是线段AB的中点,
此内容正在抓紧时间编辑中,请耐心等待
孙老师
男,中教高级职称
在教学中勤恳敬业,教学成绩优异,多次被评为“优秀数学教师”称号。























