课程内容
《空间向量及其加减运算》
学习目标
1、理解空间向量的概念,掌握空间向量的加法运算。
2、用空间向量的运算意义和运算解决立体几何问题。
重点:空间向量的加法、减法运算律。
难点:作向量解决立体几何问题。
引入
如图(1):已知OA=6米,AB=6米,BC=3米,那么OC=?
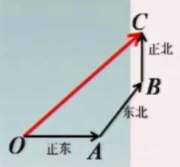 (1)
(1) (2)
(2)
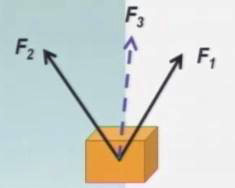
已知F1=2000N,F2=2000N,F3=2000N。
这三个呼两两之间的夹角都为60度,它们的合力的大小为多少N?
一、空间向量的有关概念
空间向量:在空间中,具有大小和方向的量。
常用(→,a)、(→,b)、(→,c)……等小写字母表示。
1、向量(→,a)的大小叫做向量的长度或模,记作∣(→,a)∣
类似于平面向量,为了研究的方便起见我们规定:
零向量、单位向量,相等向量、相反向量,平行向量、共面向量等概念。(你认为应该怎样规定?)
空间向量的加减法运算
| 平面向量 | 空间向量 | |
| 概念 | 定义:具有大小、方向的量,表示法、相等向量 | |
| 加法减法运算 |
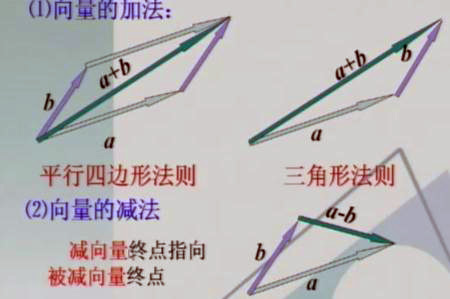
加法:三角形法则或平行四边形法则 |
加法:三角形法则或平行四边形法则 减法:三角形法则 |
| 运算律 | 加法交换律 (→,a)+(→,b)=(→,b)+(→,a) 加法结合律 {(→,a)+(→,b)}+(→,c)=(→,a)+{(→,b)+(→,c)} |
加法交换律 (→,a)+(→,b)=(→,b)+(→,a) 加法结合律{(→,a)+(→,b)}+(→,c)=(→,a)+{(→,b)+(→,c)} |
3、空间向量的加减法
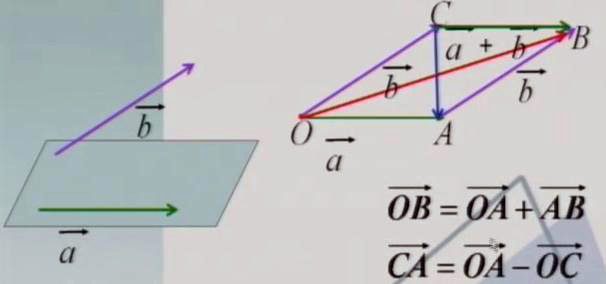
2、平面向量的加减运算结论:空间任意两个 向量的是共面向量,所以它们可用同一平面内的两条有向线段表示。
因此凡是涉及空间任意向量的问题,平面向量中有关结论仍适用于它们。
始点相同的三个不共面向量之和,等于以这三个向量为棱的平行六面体的以公共始点为始点的对角线所示向量。




























