课程内容
《函数的极值与导数》
(一)复习
一般地,函数y=f(x)在某个区间(a,b)内
1)如果恒有f′(x)﹥0,那么y=f(x)在这个区间(a,b)内单调递增;
2)如果恒有f′(x)<0,那么y=f(x)在这个区间(a,b)内单调递减;
f′(x)﹥0 增函数
f′(x)<0 减函数
判定函数单调性的常用方法:
(1)定义法
(2)导数法
(二)探究、
如图,函数y=f(x)在a、b、c、d、e、f、g、h、i等点的函数值与这些点附近的函数值有什么关系,y=f(x)在这些点的导数值是多少?在这些点附近,y=f(x)的导数的符号有什么规律?
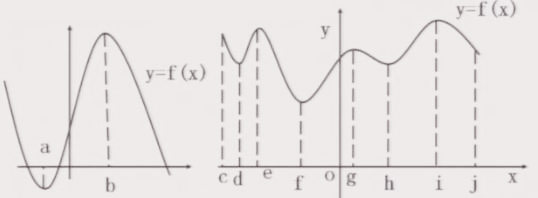
(三):讲授新课 a)函数极值的定义
1)函数y=f(x)在x=a处的函数值f(a)比它在点x=a附近其它各点的函数都小,我们就说f(a)是函数的一个极小值,点a叫做极小值点。
2)函数y=f(x)在x=b处的函数值f(b)比它在点x=b附近其它各点的函数值都大,我们就说f(b)是函数的一个极大值,点b叫做极大值点。
3)极大值点,极小值点统称为极值点,
4)极大值与极小值统称为极值。
注:函数的极大值、极小值未必是函数的最大值、最小值。
即:极大值不一定等于最大值;极小值不一定等于最小值。
b)求函数的极值
1)如果b是f′(x)=0的一个根,并且在b的左侧附近f′(x)﹥0,在右侧f′(x)<0,那么f(b)是函数f(x)的一个极大值。
2)如果a是f′(x)=0的一个根,并且在a的左侧附近f′(x)<0,在a右侧附近f′(x)﹥0,那么f(a)是函数f(x)的一个极小值。
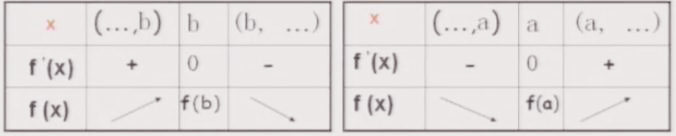
C)注意:
(1)函数的极值是就函数在某一点附近的小区间而言的,在函数的整个定义区间内可以能有多个极大值或极小值。
(2)极大值不一定比极小值大,
(3)要区分极值与极值点;
(4)导数等于零的点不一定是极值点。
例:y=x3
d)求函数极值的一般步骤:
(1)确定函数的定义域
(2)求方程f′(x)=0的根
(3)用方程f′(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格
(4)由f′(x)在方程f′(x)=0的根左右的符号,来判断f(x)在这个根处取极值的情况。
口诀:左负右正为极小,左正右负为极大。
e)例题讲解
例1:下图是导函数y=f′(x)的图象,在标记的点中,在哪一点处
(1)导函数y=f′(x)有极大值?
x=x2
(2)导函数y=f′(x)有极小值?
x=x1或x=x4
(3)函数y=f(x)有极大值?
x=x2
(4)函数y=f(x)有极小值?
x=x5
例2:求函数f(x)1/3x3-4x+4的极值
解:
因为f(x)=1/3x3-4x+4,所以f′(x)=x2-4
令f′(x)=0,解得x=2,或x=-2。
当f′(x)﹥0,即x﹥2,或x<-2;
当f′(x)<0,即-2<x<2。
当x变化时,f(x)的变化情况如下表:
| x | (-∞、-2) | -2 | (-2、2) | 2 | (2、+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | 28/3 | 单调递减 | -4/3 | 单调递增 |
所以,当x=-2时,f(x)有极大值28/3;
当x=2时,f(x)有极小值-4/3。
例3:求下列函数的极值:
(1)f(x)=6x2-x-2; (2)f(x)=x3-27x,
解:
(1)f′(x)=12x-1,令f′(x)=0,解得x=1/12,列表:
| x | ( -∞,1/12) | 1/12 | (1/12,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 单调递减 | 单调递增 |
所以,当x=1/12时,f(x)有极小值f(1/12)=-49/24。
解:
(2)令f′(x)=3x2-27=0,解得x1=3,x2=-3列表:
| x | ( -∞,-3) | -3 | (-3,3) | 3 | (3,+∞) |
| f′(x) | 0 | 0 | |||
| f(x) |
(四):课堂练习
求下列函数的极值
(1)f(x)=6+12x-x3; (2)f(x)=3x-x3。
(1)当x=-2时,f(x)有极小值-10;
当x=-1时,f(x)有极大值22。
(1)当x=-2时,f(x)有极小值-2;
当x=1时,f(x)有极大值2。
思考题:求函数y=1/4x4-4/3x3+2x2+5的极值



























