课程内容

《抛物线及其标准方程》
椭圆、双曲线的第二定义
平面内与一个定点的距离和一条定直线的距离的比是常数e的点的轨迹。
当0＜e＜1时，是椭圆；
当e﹥1时，是双曲线。
当e=1时，它又是什么曲线呢？
1、抛物线的定义
平面内与一个定点F和一条直线L的距离相等的点的轨迹叫做抛物线。
定点F叫做抛物线的焦点；
定直线L叫做抛物线的准线。
即：若∣MF∣/∣MN∣=1，则点M的轨迹的抛物线。
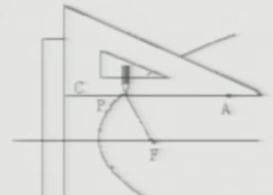
数学实验
用直尺，三角板，一条细绳，取绳长等于∣AC∣，把绳子两端固定地点A和F上，用铅笔尖扣着绳子，使点A到笔尖的一段绳子紧靠着三角尺，然后将三角尺沿着直尺上下滑动，毛尖就在图板上描出了戋要曲线。

2、抛物线的标准方程
求曲线方程的基本步骤是怎么样的？
建系 设点 列式 化简 证明
2-1、抛物线的标准方程的推导
高一个定点到一条直线L的距离为常数P（P﹥0）即∣KF∣=P，如何建立直角坐标系，求出抛物线的方程呢？

探索一：以L为y轴，过点F且垂直于L的直线为x轴建立直角坐标系，则点F（P，0）。
设动点M（x,y）,由抛物线定义得
√（x-P）²+y²=∣x∣
化简得y²=2Px-p²(P﹥0)
探索二：以定点F为原点，过点F且垂直于L的直线为x轴建立直角坐标系，
由点F（0，0），L的方程为x=-P。
√x²+y²=∣x+P∣
化简得
y²=2Px+P²(P﹥0)。
探索三：取过点F且垂直于L的直线为x轴，以线段KF的垂直平分线为y轴建立直角坐标系。
建立直角坐标系，设∣KF∣=P（P﹥0）
那么焦点F的坐标为（P/2,0）准线L的方程为x=-P/2
设抛物线上的点M（x，y），则有
∣MF∣=∣MD∣√（x-P/2）²+y²=∣x+P/2∣
（x-P/2）²+y2=x²+Px+P²/2
y²=2Px（P﹥0）
表示焦点在x轴的正半轴上的抛物线。
一般地，我们把顶点在原点、焦点F在坐标轴上的抛物线的方程叫做抛物线的标准方程
y²=2Px（P﹥0）
表示的抛物线，其焦点F位于x轴的正轴上，其准线交于x轴的负半轴。
其中P为正常数，它的几何意义是：焦点到准线的距离（焦准距）
焦点F：（P/2，0）准点L的方程：x=-P/2
但是，一条抛物线，由于它在坐标平面内的位置不同，方程也不同，所以抛物线的标准方程一定有其它的形式。

图象	开口方向	标准方程	焦点	准线
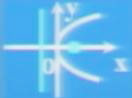	向右	y2=2Px（P﹥0）	F=（P/2，0）	x=-（P/2）
	向左	y2=-2Px（P﹥0）	F=（-P/2，0）	x=（P/2）
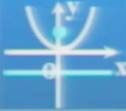	向上	x2=2Py（P﹥0）	F=（0，P/2）	y=-（P/2）
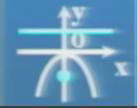	向下	x2=-2Py（P﹥0）	F=（0，-P/2）	y=（P/2）