课程内容
《双曲线的简单几何性质》
一、复习回顾
1、双曲线的定义
平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于∣F1F2∣)的点的轨迹叫做双曲线,这两个定点叫做双曲线的焦点,两焦点的距离叫做双曲线的焦距。即∣∣MF1∣-∣MF2∣∣=2a,(2a<2c)
2、双曲线的标准方程:
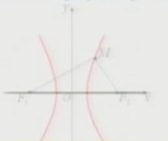
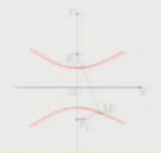
x2/a2-y2/b2=1(a﹥0,b﹥0) y2/a2-x2/b2=1(a﹥0,b﹥0)。
3、前面我们学习了椭圆的哪些几何性质?
你能类比探究出双曲线的几何性质吗?
| 性质 方程 | x2/a2-y2/b2=1(a﹥0,b﹥0) | y2/a2-x2/b2=1(a﹥0,b﹥0) |
| 图形 | ||
| 范围 | -a≤x≤a,-b≤y≤b | |
| 对称性 | 关于x,y轴用原点对称 | |
| 顶点坐标 | A1(-a,0),A2(a,0) B1(0,-b),B2(0,b) A1A2叫长轴,B1B2叫短轴 |
|
| 离飞信率 | e=c/a,(0<e<1) |
一、研究双曲线x2/a2-y2/b2=1(a﹥0,b﹥0)的笑意几何性质
1、范围
因为x2/a2≥1,x2≥a2
∴x≥a,x≤-a
2、对称性
关于X轴,Y轴和原点都是对称。
X轴、Y轴是双曲线的对称轴,原点是对称中心,叫做双曲线的中心
3、顶点
(1)双曲线与对称轴的交点,叫做双曲线的顶点。
顶点是A1(-a,0)、A2(a,0)
(2)线段A1B2叫做双曲线的实轴,
线段B1B2叫做双曲线的虚轴。
实轴的长为2a,虚轴的长为2b;
a称为半实轴的长,b称为半虚轴的长;
(3)实轴与虚轴等长的双曲线叫等轴双曲线。
x2-y2=m(m≠0)
4、渐近线
(1)双曲线x2/a2-y2/b2=1(a﹥0,b﹥0)的渐近线为y=±(b/a)x
(2)等轴双曲线x2-y2=m(m≠0)的渐近线为y=±x
双曲线的渐近线
规定:直线y=±(b/a)x叫做双曲线x2/a2-y2/b2=1的渐近线。
思考:①双曲线x2/a2-y2/b2=1的渐近线方程是什么?y=±(a/b)x
②两种双曲线的渐近线方程,怎么统一记忆?
x2/a2-y2/b2=1 x2/a2-y2/b2=0 y=±(b/a)x
y2/a2-x2/b2=1 y2/a2-x2/b2=0 y=±(a/b)x
3、双曲线的画法
①定顶点
②画矩形
③画渐近线
5、离以率
(1)定义:双曲线的焦距与实轴长的比e=c/a,叫做双曲线的离以率。
(2)e的范围:因为c﹥a﹥0 ∴e﹥0
(3)e的含义:b/a=(√c2-a2)/a=√(c/a)2-1=√e2-1
∴当e∈(1+∞)时,b/a∈(1+∞),且e增大,b/a也增大。 e增大时,渐近线与实轴的夹角增大。
e是表示双曲线开口大小的一个量,e越林开口越大。
此内容正在抓紧时间编辑中,请耐心等待
朱老师
男,中教高级职称
对高中数学的基本概念和整体知识结构有清晰地把握,从高考的高度分析讲解各大知识板块。
























