课程内容
《椭圆的简单几何性质(一)》
教学目的：
1、熟练掌握椭圆的范围，对称性，顶点等简单几何性质
2、掌握标准方程中a，b，c的几何意义，以及a，b，c，e的相互关系
3、理解、掌握坐标法中根据曲线的方程研究曲线的几何性质的一般方法
教学重点：椭圆的几何性质
教学难点：如何贯彻数形结合思想，运用曲线方程研究几何性质
复习：
1、椭圆的定义：
平面内与两个定点F_1、F₂的距离和等于常数（大于F₁F₂）的点的轨迹叫作椭圆。
|PF₁|+|PF₂|=2a（2a>|F₁F₂|）
2、椭圆的标准方程是：
当焦点在X轴上时：x²/a²+y²/b²=1(a>b>0)
当焦点在Y轴上时：y²/a²+x²/b²=1(a>b>0)
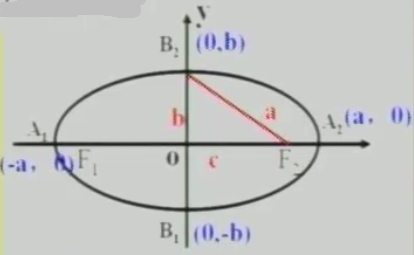
3、椭圆中a，b，c的关系是：
a²=b²+c²

	焦点在X轴上	焦点在Y轴上
不同点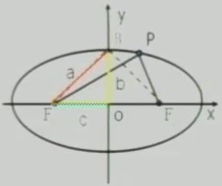
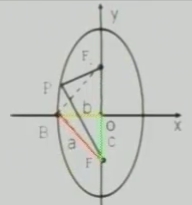	F1（-c，0）F2(c,0)	F1（0,-c）F2(0,c)
	x2/a2+y2/b2=1(a>b>0)	y2/a2+x2/b2=1(a>b>0)
相同点	定义：PF1+PF2=2a
	参数：a2=b2+c2（a>b>0  a>c>0）

二、椭圆x²/a²+y²/b²=1简单的几何性质
1、范围：x²/a²≤1，y²/b^2≤1得：
-a≤x≤a，-b≤y≤b知
椭圆落在x=±a，y=±b组成的矩形中

2、椭圆的对称性
从图形上看，拖延关于X轴，Y轴、原点对称。
从方程上看：
（1）把X换成-X方程不变，图象关于Y轴对称；
（1）把Y换成-Y方程不变，图象关于X轴对称；
（1）把X换成-X方程不变，同时把把Y换成-Y方程不变，图象关于原点成中心对称。
3、椭圆的顶点
x²/a²+y²/b²=1(a>b>0)
令X=0，得Y=？，说明椭圆与Y轴的交点？
令Y=0，得X=？说明椭圆与X轴的交点？
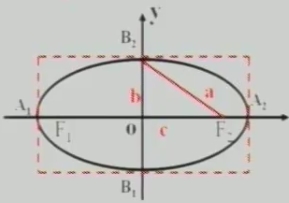
顶点：椭圆与它的对称轴的四个交点，叫做椭圆的顶点。
长轴、短轴：线段A₁A₂、B₁B₂分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。

根据前面所学有关知识画出下列图形
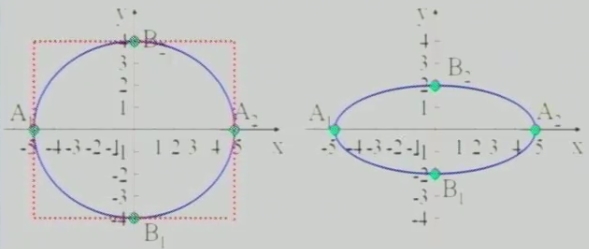
（1）x²/25+y²/16=1
（2）x²/25+y²/4=1

4、椭圆的离心率e（刻画椭圆扁平程度的量）
离心率：椭圆的焦距与长轴长的比：e=c/a叫做椭圆的离心率。
（1）离心率的取值范围：0 （2）离心率对椭圆形状的影响：
1）e越接近1，c就越接近a，从而b就越小，椭圆就越扁。
2）e越接近0，c就越接近0，从而b就越大，椭圆就越圆。
思考：当e=0时，曲线是什么？当e=1时，曲线又是什么？
|3|e与a,b的关系：e=c/a=√（(a-b)/c）=对（1-b/a）
问：对于椭圆C₁：9x²+y²=36与椭圆C₂：x²/16+y²/12=2更接近于圆的是：C₂

标准方程	x2/a2+y2/b2=1(a>b>0) y2/a2+x2/b2=1(a>b>0)
范围	|x|≤a，|y|≤b
对称性	关于x轴对称，y轴成轴对称；关于原点成中心对称
顶点坐标	（a，0）（-a,0）,(0,b)(0,-b)
焦点坐标	（c,0）、(-c,0)
半轴长	长半轴长为a，短半轴长尾b,a＞b
离心率	e=c/a
a、b、c的关系	a2=b2+c2

例1、已知椭圆方程为16x²+25y²=400，则它的长轴长是：10；短轴长是：8；焦距是：6；离心率等于：3/5；焦点坐标是：（±3,0）；顶点坐标是：（±5,0）（0，±4）：外切矩形的面积等于：80；