课程内容

《椭圆及其标准方程（二）》
复习旧知
1、椭圆的定义：
平面内与两个定点F₁F₂的距离和等于常数（大于F₁F₂）的点的轨迹叫作椭圆，这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距。
注：若P是椭圆的点，则
|PF₁|+|PF₂|=2a
2、椭圆的标准方程

定义	|MF1|+|MF2|=2a(2a>2c>0)
图形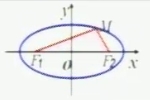
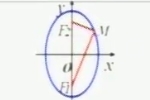方程	x2/a2+y2/b2=1(a>b>0)	y2/a2+x2/b2=1(a>b>0)
焦点	F1（-c,0）,F2(c,0)	F1(0,-c),F2(0,c)
a、b、c之间的关系	a2-c2=b2(a>b>c>0,a>b>0)

注：焦点位置的判断
看分母的大小，焦点在分母大的那一项对应的坐标轴上。
旧知测试：
1、如果方程x²+ky²=1表示焦点在y轴上的椭圆，那么实数k的取值范围是（D）
A、（0，+∞）
B（0,2）
C、（1，+∞）
D（0,1）
2、椭圆x²/25+y²/9=1一点P到一个焦点的距离为5，则P到另一个焦点的距离（A）
A、5   B、6   C、4   D、10
3、椭圆x²/25+y²/169=1的焦点坐标是（C）
A(±5,0)   B（0，±5）   C（0，±12）    D（±12,0）
4、已知椭圆方程为x²/23+y²/32=1，则这个椭圆的焦距为（A）
A、6   B、3   C、3√5   D、8
5、F₁F₂是定点，且|F₁F₂|=6，动点M满足|MF₁|+|MF₂|=6，则点M的轨迹是（D）
A、椭圆
B、直线
C、圆
D、线段
例1：如图，设点A、B的坐标分别为（-5,0）（5，0），直线AM，BM相较于点M，且它们的斜率之积是-4/9，求点M的轨迹方程。

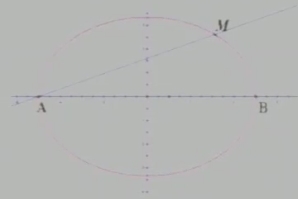
解：设M（x,y）
由题可得：
y/(x=5)·y/(x-5)=-(4/9)
y²/(x²-25)=-(4/9)
9y²=100-4x²
9y²⁺4x²=100
∴点M的轨迹方程为：x²/25+y²/(100/9)=1
例2、如图，在圆x²+y²=4上任取一点P作x轴的垂线段PD，D为垂足。当点P在圆上运动时，线段PD的中点M的轨迹是什么？为什么？
解：设点M坐标为M（x,y），点P的坐标为P(x',y'),则
由提议可得：x'=x,y'=y
因为x'²+y'²=4
所以x²+4²y=4即x/4+y=1
这就是点M的轨迹方程，它表示一个椭圆。
例3、已知B、C两个定点，|BC|=6且三角形ABC的周长为16，求顶点A的轨迹方程。
变式1：已知B（-3,0），C（3,0），|CA|、|BC|、|AB|成等差数列，求三角形ABC的顶点A的轨迹方程。
变式2：已知已知B（-3,0），C（3,0）且sinB+sinC=2sinA，求三角形ABC的顶点A的轨迹方程。
变式3：一动圆与已知圆O：（x+3）+y=1外切，与圆O：（x-3）+y=81内切，试求这动圆圆心的轨迹方程。