课程内容

《椭圆及其标准方程（一）》
教学目的：
1、理解椭圆的定义、明确焦点、焦距的概念。
2、熟练掌握椭圆的标准方程，会根据所给的条件画出椭圆的草图并确定椭圆的标准方程。
3、能由椭圆定义推到椭圆的方程。
4、启发学生能够发现问题和提出问题，善于独立思考，学会分析问题和创造地解决问题；培养学生抽象概括能力和逻辑思维能力。
教学重点：椭圆的定义和标准方程
教学难点：椭圆标准方程的推导
一、情景引入
问题：2008年9月28日上午9时，“神舟七号”载人飞船顺利升空，实现多人航天飞行，标志着我国航天事业又上了一个新台阶，请问：“神舟七号”飞船的运行轨道是什么？
生活中还有哪些东西像椭圆呢？
二、实验操作
1、玻璃杯装半杯水，适度倾斜，观察水面是个什么形状？
2、手工操作演示椭圆的形成：取一条定长的细绳，把它的两端固定在画图板上的两点，当绳长大于两点间的距离时，用铅笔把绳子拉近，使笔尖在图板上慢慢移动，就可以画出一个椭圆。
椭圆的形成：


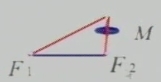
取一条长尾2a的细绳，把它的两端固定在画图板上的F₁和F₂两点，用铅笔尖把绳子拉紧，使笔尖在图板上慢慢移动。
椭圆的定义：
平面内与两个定点F₁、F₂的距离的和等于常数（大于|F₁F₂|）的点的轨迹叫做椭圆。
这两个定点F_1、F₂叫做椭圆的焦点，两焦点的距离叫做椭圆的焦距（一般用2c表示）。
|MF₁|+|MF₂|=2a
三、定义形成
平面内与两个定点F₁、F₂的距离的和等于常数（大于|F₁F₂|）的点的轨迹叫做椭圆。这两个定点叫做椭圆的焦点，两焦点的距离叫做椭圆的焦距。
椭圆的定义的再认识
问题：假设与两定点的距离之和为d，为什么要满足d>2c呢？
（1）当d=2c时，轨迹是什么？
（2）当d<2c时，轨迹又是什么？
结论：当d>|F₁F₂|时，是椭圆；
当d=F₁F₂时，是线段；
当d1F₂，轨迹不存在；
那么，如何求椭圆的方程呢？
如图所示：F₁、F₂为两定点，且|F₁F₂|=2c，求平面内到两定点F₁、F₂距离之和为定值2a(2a>2c)的动点M的轨迹方程。

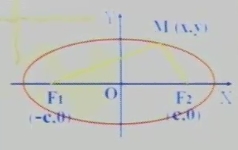
解：以F₁、F₂所在直线为X轴，F₁、F₂的重点为原点建立平面直角坐标系，则焦点F₁、F₂的坐标分别为（-c）、(c,0)。
设M（x,y）为所求轨迹上的任意一点，则|MF₁|+|MF₂|=2a
即：√（（x+c）²+y²）+√（（x-c）²+y²）=2a
所以：√（（x+c）²+y²）=2a-√（（x-c）²+y²）
两边平方得：：（（x+c）²+y²）=4a²-4a√（（x-c）²+y²）+(x-c)²+y²
即：a²-cx=a√((x-c)²+y²)
两边平方得：a⁴-2a²cx+c²x²=a²x²-2a²cx+a²c²+a²y²
即：(a²-c²)x²+a²y²=a²(a²-c²)
因为2a>2c，即a>c，所以a²-c²>0，令a²-c²=b²，其中b>0，代入上式可得：
b²x²+a²y²=a²b²
两边同时除以a²b²得：
x²/a²+y²/b²=1(a>b>0)

椭圆的标准方程的再认识
（1）椭圆的标准方程的形式：左边是两个分式的平方和，右边是1；
（2）椭圆的标准方程中三个参数a、b、c满足a²=b²+c²。
（3）由椭圆的标准方程可以求出三个参数a、b、c的值。
（4）椭圆的标准方程中，x²与y²的分母哪一个大，则焦点在哪一个轴上。
例题精析
例1、填空：
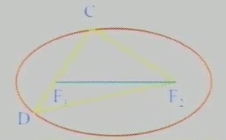
（1）已知椭圆的方程为x²/25+y²/16=1，则a=5,b=4,c=3,焦点坐标为（3,0），（-3,0）焦距等于6。若CD为过焦点F₁的弦，则F₂CD的长为20

（1）已知椭圆的方程为x²/4+y²/5=1，则a=√5,b=2,c=1,焦点坐标为（1,0），（-1,0）焦距等于2。曲线上点P到左焦点F₁的距离为3，则点P到另一个焦点F₂的距离等于2√5-3，则F₁PF₂的周长为2√5+2。
例2、求满足下列条件的椭圆的标准方程：
（1）满足a=4，b=1，焦点在X轴上的椭圆的标准方程为x²/16+y²=1
（2）满足a=4，c=√15，焦点在Y轴上的椭圆的标准方程为y²/16+x²=1
例4、化简
√（x²+(y-3)²）+√(x²+(y-3)²)=10
分析：点M（x,y）到两定点（0，-3）（0,3）的距离之和为定值10
|MF₁|+|MF₂|=10
答案x²/25+y²/16=1
例5：动点P到两定点F₁（-4,0），F₂（4,0）的距离之和为8，则动点P的轨迹为（B）
 A、椭圆
B、线段F₁F₂
C、直线F₁F₂
D、不能确定
例6：求满足下列条件的椭圆的标准方程：
两焦点的坐标分别是（-4,0）（4,0）椭圆上一点P到两焦点的距离之和等于10
解：因为焦点坐标在X轴上，所以标准方程设为：
x²/a²+y²/b²=1(a>b>0)
∵2a=10,2c=8
∴a=5,c=4
∴b²=a²-c²=5²-4²=9
所以椭圆的标准方程为：
x²/25+y²/9=1
小结：
1、椭圆的定义及焦点、焦距的概念
2、椭圆的标准方程
x²/a²+y²/b²=1(a>b>0)
y²/a²+x²/b²=1(a>b>0)
3、标准方程的简单应用