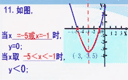
课程内容

《相似三角形》
理清知识脉络
一、比例统线段
1、若四条线段a，b，c，d中，如果a/b=c/d（或a:b=c:d），那么这四条线段a、b、c、d叫做成比例的线段，简称比例线段。
其中：a、b、c、d叫做组成比例的项，线段a、b叫做外项，线段b、c叫做内项，
比例的改天性质：a/b=c/d≌ab=bc，
2、比例中项
当两个比例中项相等时，即a/b=b/c，（或a：b=b:c）,那么线段b叫做线段a和c的比例中项；即：b²=ac
练习：
数2与8的比例中项是     。
线段2㎝与8㎝的比例中项是       。
3、黄金分割：
把一条线段（AB）分成两条线段，使其中较长线段（AC）是原线段（AB）与较短线段（BC）的比例中项，就叫做把这条线段黄金分割。即：AC2=AB×BC，AC=（√5-1）/2×AB
练习:
C是线段AB的黄金分割点，较长线段AC=2（√5-1），则AB=        。
二、相似三角形
1、相似三角形的定义：
对应角相等、对应边成比例的三角形叫做相似三角形。
2、相似比：
相似三角形的对应边的比，叫做相似三角形的相似比。
练习：
△ABC∽△AB，如果AC=4，BC=2，那么△ABC与△ABC的相似比为      。
三、相似三角形的性质
1、相似三角形的对应角相等，对应边成比例；
2、相似三角形对应高的比、对应中线的比和对应角的平分线的比都等于相似比；
3、相似三角形的周长的比等于相似比；
4、相似三角形面积的比等于相似比。
注意：利用相似三角形的性质得到对应角相等或对应线段成比例时，要注意对应关系。
四、相似三角形的判定方法
1、平行于三角形一边的直线和其它两边（或延长线）相交，所构成三角形与原三角形相似。
2、三边对应成比例的两个三角形相似；
3、两边对应成比例且夹角相等的两个三角形相似；
4、二角对应相等的二个三角形相似；
5、如果两个直角三角形的斜边和一条直角边对应的比相等，那么这两个直角三角形相似。
注意：直角三角形被斜边上的高分成的两个二个直角三角形与原三角形彼此相似。