课程内容
《二次函数概念、图像、性质》
一、二次函数的定义
1、定义:一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数。
2、定义要点:
(1)关于x的代数式一定是整数,a,b,c为常数且a≠0。
(2)等式的左边最高次数为2,可以没有一次项和常数项,但不能没有二次项。
如:y=-x2,y=2x-4x+3,y=100-5x2,y=-2x2+5x-3等等都是二次函数。
已知二次函数y=(1-m)xm2-2的图像开口向下求m的值:2
M2-2=2
1-m<0
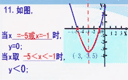
二次函数的图象及性质
|
抛物线 |
Y=ax2 |
y=ax2+c |
Y=a(x-h)2 |
Y=a(x-h)2+k |
Y=ax2+bx+c |
Y=a(x+b/2a)2+(4ab-b2)/4a |
|
|
开口方向 |
当a﹥0时开口向上,并向上无限延伸; 当a﹤0时开口向下,并向下无限延伸; |
||||||
|
顶点坐标 |
(0,0) |
(0,c) |
(h,0) |
(h,k) |
(-b/2a,(4ac-b2)/4a) |
||
|
对称轴 |
Y轴 |
Y轴 |
直线x=h |
直线x=h |
直线x=-2/2a |
||
|
最值 |
a﹥0 |
X=0时,ymin=0 |
X=0时,ymin=c |
X=h时,ymin=0 |
X=0时,ymin=k |
X=b/2a时,ymin=(4ac-b2)/4a |
|
|
a﹤0 |
X=0时,ymax=0 |
X=0时,ymax=c |
X=h时,ymax=0 |
X=0时,ymax=k |
X=b/2a时,ymax=(4ac-b2)/4a |
||
|
增减性 |
a﹥0 |
在对称轴左侧,y随x的增大而减小。 |
|||||
|
在对称轴右侧,y随x的增大而增大。 |
|||||||
|
a﹤0 |
在对称轴左侧,y随x的增大而增大。 |
||||||
|
在对称轴右侧,y随x的增大而减小。 |
|||||||
二次函数y=ax2+bx+c(a≠0)的系数a,b,c与图象的关系
|
A |
A决定开口的方向:a﹥0时,不成器向上,a﹤0时,不开口向下。 |
|
A,b |
A, b同时决定对称轴的位置:a,b同号时对称轴在y左侧; a, b同号时对称轴在y右侧; b=0时对称轴是y左侧。 |
|
c |
C决定抛物线与y轴的交点:c﹥0时抛物线交于y轴的正半轴; C=0时,抛物线过原点; c﹤0时抛物线交于y轴的负半轴。 |
总结:
1、基本概念要熟记;
2、要熟练找出二次函数的三要素,即开口方向、对称轴、项点坐标;
3、掌握二次函数的对称性及增减性。