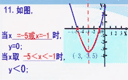
课程内容

《探索规律问题》
解题策略   → 观察、分析、归纳、验证。
题型一：关于代数问题
1、一一组数：1，2，5，10，17，26，……，请观察这组数的构成规律，用你发现的规律确定8个数为              。
2、把正确整数1，2，3，4，5，……，按如下规律排列：
1
2，3，
4，5，6，7，
8，9，10，11，12，13，14，15，
……  ……  ……
按规律，可知第N行有        个正整数。
3、古希腊数学家把1，3，6，10，15，21，……，叫做三角形数，它有一定的规律性，则第24个三角形与第22个三角形数的差为         。
4、观察下列算式：
2¹=2     2⁵=32
2²=4     2⁶=64
2³=8     2⁷=128
2⁴=16……
通过观察，用你所发现的规律确定2 27的个位数字是（   ）
A、2    B、4   C、6   D、8
5、观察下列等式：
1=1²
1+3=2²
1+3=+5=3²
……
根据观察可得：1+3+5+……+2n-1=     （n为正整数）。
6、观察下列排序的等式：
9×0+1=1
9×1+2=11
9×2+3=21
9×3+4=31
9×4+5=41
……
猜想：第n个等式（n为正整数）应为           。
题型二：关于图形规律问题：
1、为庆祝“六、一”儿童节，某幼儿园举行用火柴棒摆“金鱼”比赛。如图所示：按照上面的规律，摆n个“金鱼”需要火柴棒的概数为（   ）

A、2+6n    B、8+6n
C、4+4n    D、8n
2、下列图案是由长边为单位长度的小正方形按一定的规律拼接而成。依此规律，第5个图案中小正方形的个数为       。

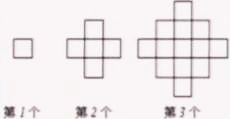
3、如图所示，一串有趣的图案按一定规律排列，请仔细观察，在前16个图案中有    个