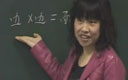课程内容

《反比例》
例题：把相同体积的水倒入底面积不同的杯子。
 高度cm    30  20  15  10  5
底面积cm²  10  15  20  30  60
 体积cm³   300 300 300 300 300
（1）表中有哪两种量？它们是不是相关联的量？
     表中有高度和底面积两种量，是相关联的量。
（2）写出几组这两种量相对应的两个数的乘积，并观察积有什么规律？
     30×10=300
     20×15=300
     15×20=300
     ……
（3）高度和底面积的变化有什么规律？
     底面积越大，水的高度越低……
     30×10=20×15=15×20=……=300，高度和底面积的乘积一定。
因为水的体积一定，所以水的高度随着底面积的变化而变化。底面积增加，高度反而降低，底面积减少，高度反而升高，而且高度和底面积的乘积一定，我们就说高度和底面积成反比例关系，高度和底面积叫做成反比例的量。
如果用字母x和y表示两种相关联的量，用k表示它们的乘积（一定），反比例关系可以用下面的式子表示：
    xy=k（一定）
怎样判断两种量成反比例：
（1）两种量是否相关联。
（2）变化规律是否一致。
（3）相对应的两个量的积是否一定。
路程一定，判断速度和时间是否成反比例。
练习
1、填空。
（1）两种（    ）的量，一种量变化，另一种量也（    ），如果这两种量中相对应的两个数的（   ）一定，这两种量就叫做成（     ），它们的关系叫做（       ）。
（2）用字母表示两个量的反比例关系（          ）。
2、判断下面每题中的两种量是不是成反比例？说明理由。
（1）工作总量一定，工作效率和工作时间。
（2）长方形的面积一定，长和宽。
（3）全校人数一定，男生人数和女生人数。
（4）物品的总价一定，物品的单价和数量。
（5）铁丝的长度一定，剪去的和剩下的。
（6）跑步的速度和时间。
3、按要求填空。
（1）路程一定，（   ）和（   ）成反比例。
（2）总价一定，（   ）和（   ）成反比例。
（3）（   ）一定，（   ）和（   ）成反比例。
4、如果A×B=C，那么：
C一定，A和B成（   ）比例。
B一定，A和C成（   ）比例。
A一定，B和C成（   ）比例。
小结
正比例和反比例的比较：
相同点：1、都有两种相关联的量
        2、一种量随着另一种量变化
不同点：
正比例：1、变化方向相同，一种量扩大或缩小，另一种量也扩大或缩小。
        2、相对应的每两个数的比值（商）是一定的。
反比例：1、变化方向相反，一种量扩大（缩小），另一种量反而缩小（扩大）。
        2、相对应的每两个数的积是一定的。