课程内容

《数据的波动》
温故知新
数据的统计中，反应数据的“平均水平”的量
平均数、中位数、众数
问题情境
为了提高农副产品的国际竞争力，一些行业协会对农副产品的规格进行了划分。某外贸公司要进口一批规格为75g的鸡腿，现有2个厂家提供货源，它们的价格相同鸡腿的品质也相近。
质检员分别从甲、乙两厂的产品中抽样调查了20只鸡腿，它们的质量（单位：g）如表。根据表绘制成了图。
（1）你能从图中估计出甲、乙两厂被抽取的鸡腿的平均质量吗？
（2）求甲乙两厂被抽取的鸡腿的平均质量，并在图中画出来表示平均质量的直线。
（3）从甲厂抽取的这20只鸡腿质量的最大值是多少？最小值又是多少？它们相差几克？乙厂呢？
新知探究1
实际生活中，除了关心数据的“平均水平”外，人们往往还关注数据的离散程度，即它们相对于“平均水平”的偏离情况。极差就是刻画数据的离散程度的一个统计量。
极差是指一组数据中最大数据与最小数据的差。
巩固概念
1、样本3，4，2，1，5的平均数为____，中位数为____，极差为____。
2、在数据统计中，能反映一组数据变化范围大小的指标是（   ）
   A、平均数   B、众数   C、中位数   D、极差
3、某日最高气温是4℃，温差是9℃，则最低气温是____℃。
4、公园有两条石级路，第一条石级路的高度分别是（单位：cm）：15，16，16，14，15，14；第二条石级路的高度分别是11，15，17，18，19，10，哪条路走起来更舒服？
新知探究2
如果丙厂也参与了竞争，从该厂抽样调查了20只鸡腿，数据如下图所示。
（1）丙厂这20只鸡腿质量的平均数和极差分别是多少？
（2）如何刻画丙厂这20只鸡腿质量与其平均数的差距？分别求出甲、丙两厂的20只鸡腿质量与其相应平均数的差距。
概念分析
你能举出生活中用到极差的例子吗？
极差是最简单的一种度量数据波动情况的量，但只能反映数据的波动范围，不能衡量每个数据的变化情况，而且受极端值的影响较大。
数学上，数据的离散程度还可以用方差和标准差来描述。
方差是各个数据与平均数之差的平方的和的平均数。

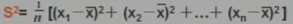
标准差就是方差的算术平方根。
方差用来衡量一批数据的波动大小。（即这批数据偏离平均数的大小）
一般地，方差越小，说明这组数据的平均数的代表性越大这组数据就越稳定。
公式应用
例：计算下列数据的方差：
    3  3  4  6  8  9  9
计算方差的步骤可概括为“先平均，后求差，平方后，再平均”。
1、样本方差的作用是（   ）
   A、表示总体的平均水平       B、表示样本的平均水平
   C、准确表示总体的波动大小   D、表示样本的波动大小
2、样本5、6、7、8、9的方差是____。
3、在样本方差的计算公式S²=1/10[(x₁-20)²+(x₂-20)²+…+(x_n-20)²]，数字10表示________，数字20表示________。
学以致用
在一次芭蕾舞比赛中，甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》，参加表演的女演员的身高（单位：cm）分别是：
  甲团  163  164  164  165  165  165  166  167
  乙团  163  164  164  165  166  167  167  168
哪个芭蕾舞团女演员的身高更为整齐？
新知应用
气象部门记录的某天，A、B两地气温变化如下图所示：
A、B两地的气候各有什么不同？
某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛，在最近的10词选拨赛中，他们的乘积（单位：cm）如下：
  甲  585  596  610  598  612  597  604  600  613  601
  乙  613  618  580  574  618  593  585  590  598  624
（1）他们的平均成绩分别是多少？
（2）甲、乙这10次比赛成绩的极差、方差分别是多少？
（3）这两名运动员的运动成绩各有什么特点？
（4）历届比赛表明，成绩达到5.96m就有可能夺冠，你认为为了夺冠应选谁参加这项比赛？如果历届比赛成绩表明，成绩达到6.10m就能打破记录，那么你认为为了打破记录应选谁参加这项比赛？
数理统计的基本思想：用样本估计总体。
·用样本的某些特性估计总体相应的特性。
·用样本的平均数、中位数和众数去估计相应总体的平均水平特性。
·用样本的频数、频率、频数分布表、频数分布直方图和频数分布折线图去估计相应总体数据的分布情况。
·用样本的极差、方差或标准差去估计相应总体数据的波动情况。