课程内容

《展开与折叠》（一）
学习目标
1、经历展开与折叠、模型制作等活动，发展空间概念，积累数学活动经验。
2、从棱柱的侧面展开图中认识棱柱的某些特性。
做一做
如图示，左边的图形经过折叠能围成右边的棱柱吗？
1、这个棱柱的上、下底面的形状和大小一样吗？它们各有几条边？
2、这个棱柱有几个侧面？侧面的形状是什么图形？
3、侧面的个数与底面图形的边数有什么关系？
在棱柱中，任何相邻两个面的交线都叫做棱，相邻两个侧面的交线叫做侧棱。
归纳
人们通常根据棱柱底面的边数，将棱柱分为三棱柱、四棱柱、五棱柱、六棱柱……
它们的底面形状分别为三角形、四边形、五边形、六边形……
长方体和立方体都是四棱柱。
探究
1、如图示，哪些图形经过折叠可以围成一个棱柱？先想一想、再折一折。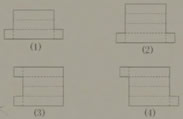

2、一个六棱柱模型如图示，它的底面边长都是5厘米，侧棱长4厘米，观察这个模型，回答下列问题：
（1）这个六棱柱一共有多少个面？它们分别是什么形状？哪些面的形状、大小完全相同？
（2）这个棱柱一共有多少条棱？它们的长度分别是多少？
探究
      三棱柱  四棱柱  五棱柱  六棱柱
面数     5       6       7       8
棱数     9      12      15      18
顶点     6       8      10      12
则n棱柱有(n+2)个面，3n条棱，2n个顶点。
随堂练习
1、如图是一个长方体模型，观察这个模型，并回答：
（1）长方体有______个顶点，______条棱，______个面，这些面的形状都是______。
（2）哪些面的形状与大小一定完全相同？
（3）哪些棱的长度一定相等？
2、棱柱的每个侧面都是______形，棱锥的每个侧面都是______形，棱柱和棱锥的底面都是______形。
3、下面的结论中，错误的是（   ）
   A、棱柱的顶点数一定是偶数
   B、棱柱的棱数一定是3的倍数
   C、棱柱的面数一定是偶数
   D、棱柱的侧面数与侧棱数一定相同
4、下面四个图形中，可以折叠成棱柱的是（   ）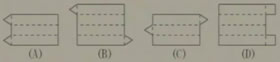

5、下列四个图形经过折叠，可以得到右面几何体的是（   ）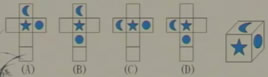

6、哪种几何体的表面能展开成下面的图形？先想一想，再折一折。
7、图中的两个图形经过折叠能否成棱柱？先想一想，再折一折。
归纳
1、从棱柱的展开图中了解到：棱柱的底面是多边形，侧面是长方形。
2、棱柱的顶点数、棱数、侧棱数的关系：顶点数是侧棱数的2倍，棱数是侧棱数的3倍。