课程内容

《用公式法解一元二次方程》
回顾与复习1 配方法
我们通过配成完全平方式的方法，得到了一元二次方程的根。这种解一元二次方程的方法称为配方法。
用配方法解一元二次方程的知识基础：
平方根的意义：如果x²=a（a≥0），那么x=±√a
完全平方式：式子a²±2ab+b²叫完全平方式，且a²±2ab+b²=(a±b)²
配方法解一元二次方程的步骤：
（1）化1：把二次项系数化为1；
（2）移项：把常数项移到方程的右边；
（3）配方：方程两边都加上一次项系数绝对值一半的平方；
（4）变形：方程左边写成完全平方式，右边合并同类项；
（5）开方：根据平方根意义，方程两边开平方。
公式法
一般地，对于一元二次方程ax²+bx+c=0(a≠0)
当b²-4ac≥0时，它的根是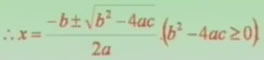

上面这个式子称为一元二次方程的求根公式。
用求根公式解一元二次方程的方法称为公式法。
用公式法解一元二次方程的前提是：1、把一元二次方程化为一般形式确定a、b、c的值。2、b²-4ac≥0。
例1：用公式法解方程2x²+5x-3=0。
用公式法解一元二次方程的一般步骤：
（1）把方程化成一般形式，并写出a、b、c的值。
（2）求出b²-4ac的值。
（3）代入求根公式。
（4）写出方程的解。
例2：解方程x²+3=(2√3)x
例3：解方程(x-2)(1-3x)=6
归纳：当b²-4ac＞0时，方程ax²+bx+c=0(a≠0)有两个不相等的实数根。
当b²-4ac=0时，方程ax²+bx+c=0(a≠0)有两个相等的实数根，x₁=x₂=-b/2a。
当b²-4ac＜0时，方程ax²+bx+c=0(a≠0)没有实数根。
当b²-4ac≥0时，方程ax²+bx+c=0(a≠0)有两个实数根。
动手试一试
1、方程3x²+1=(2√3)x中，b²-4ac=_________
2、若关于x的方程x²-2nx+3n+4=0有两个相等的实数根，则n=_________
3、练习，用公式法解方程。
（1）(3/2)x²-(1/2)x-1=0
（2）x²-(2√2)x+2=0