课程内容：

《平方差公式》
探究：计算下列多项式的积，你能发现什么规律？
    （1）（x+1）（x-1）=________；（2）（m+2）（m-2）=_________；
    （3）（2x+1）（2x-1）=_____________。
一般地，我们有  （a+b）（a-b）=a²-b²
即两个数的和与这两个数的差的积，等于这两个数的平方差。这个公式叫做（乘法的）平方差公式。
讨论：你能根据下图中的面积说明平方差公式吗？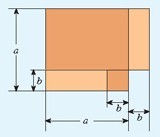

例1：运用平方差公式计算：
（1）（3x+2）（3x-2）；    （2）（b+2a）（2a-b）
（3）（-x+2y）（-x-2y）
例2.计算：
（1）102×98；    （2）（y+2）（y-2）-（y-1）（y+5）
练习：
1.下面各式的计算对不对？如果不对，应当怎样改正？
（1）（x+2）（x-2）=x²-2；（2）（-3a-2）（3a-2）=9a²-4
2.运用平方差公式计算：
（1）（a+3b）（a-3b）；    （2）（3+2a）（-3+2a）；
（3）51×49；    （4）（3x+4）（3x-4）-（2x+3）（3x-2）
思维延伸：
    已知两个正方形的周长之和等于32cm，它们的面积之差为48cm²，求这两个正方形的边长。
创新应用：
如图，在边长为a的正方形中挖掉一个边长为b的正方形（a>b）。把余下的部分剪成一个矩形（如图2），通过计算两个图形（阴影部分）的面积，验证了一个等式，这个等式是（    ）。
    A.a²-b²=(a+b)(a-b)    B.(a+b)²=a²+2ab+b²
    C.(a-b)²=a²-2ab+b²    D.(a+2b)(a-b)=a²+ab-2b²
综合拓展：
    1.计算2004²-2003×2005；
    2.请你利用平方差公式求出（2+1）（2²+1）（2⁴+1）（2⁸+1）…（2⁶⁴+1）的值。