【此视频课程与人教版第15课的知识点相同，同样适用于鲁教版第1课，敬请放心学习。】

课程内容：

《幂的乘方与积的乘方》
回顾思考：
    幂的意义：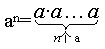
    同底数幂乘法的运算法则：a^m×aⁿ=a^m+n
练习：根据乘方的意义与同底数幂的乘法填空，看看计算的结果有什么规律？
    （1）（3²）³=（ ）×（ ）×（ ）=3^（）
    （2）（a²）³=（ ）×（ ）×（ ）=a^（）
    （3）（a^m）³=（ ）×（ ）×（ ）=a^（）（m为正整数）
    对于任意底数a与任意正整数m、n
   
    幂的乘方运算法则：（a^m）ⁿ=a^mn （m、n都是正整数）
探索：（1）根据乘方意义（幂的意义），（ab）³表示什么？
      （2）为了计算（化简）算式ab·ab·ab，可以应用乘法的交换律和结合律。
      （3）由特殊的（ab）³=a³b³出发，你能想到一般的公式吗？
           （ab）ⁿ=aⁿbⁿ
归纳：积的乘方法则：（ab）ⁿ=aⁿbⁿ（m，n都是正整数）
      积的乘方等于积中每个因式分别乘方后的积。
思考：你能说出法则中“因式”这两个字的意义吗？（a+b）ⁿ可以用积的乘方法则计算吗？
例1：计算
（1）（3x）²  （2）（-2b）⁵  （3）（-2xy）⁴  （4）（3a²）ⁿ
归纳：当积中出现多个因式时，积的乘方法则依然成立。（abc…z）ⁿ=aⁿ·bⁿ·cⁿ…zⁿ
练习：计算
（1）（-3n）³；  （2）（5xy）³；  （3）-a³+（-4a）²a
    反向使用法则：aⁿbⁿ=（ab）ⁿ
智能训练：
    1.不用计算器，你能很快求出下列各式的结果吗？
    2⁵×3×5⁵          （-4）⁹×（0.25）¹⁰
    2.若n是正整数，且xⁿ=6，yⁿ=5，求（xy）²ⁿ的值。
    3.[（a-b）（c-d）]ⁿ等于什么？写出推理过程。
总结：
    幂的意义：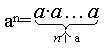
    同底数幂的乘法运算法则：a^m·aⁿ=a^m+n
    幂的乘方运算法则：（ab）ⁿ=aⁿbⁿ
    积的乘方=每个因式分别乘方后的积。