课程内容

《二次函数y=ax²的图象和性质》
函数图象的作法
描点法 列表——描点——连线

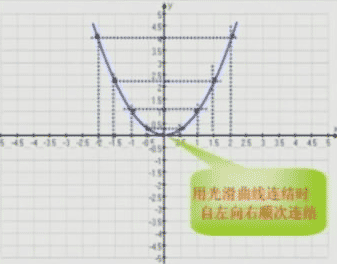
继续探究，找出二次函数y=ax²的图象的性质
在同一直叫坐标系中，画出函数y=x²，y=-x²,y=2x²与y=-2x²的图象。

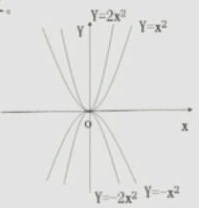
1.由函数y=x²，y=2x²的图象的共同特点，可得出：
函数y=ax²的图象是一条抛物线，它关于y轴对称，它的顶点坐标是（0,0）
当a＞0，抛物线y=ax²开口上，a越大，抛物线的开口越小，在对称轴的左边，y随x的增大而减小；在对称轴的右边，y随x的增大而增大，顶点是抛物线的最低点，也就是说当x=0时，y有最小值。
2.观察函数y=-x²、y=2x²的图象，作出类似的概括；
当a＜0时，抛物线y=x²开口向下，a越大，抛物线的开口越大，在对称轴的左边，y随x的增大而增大；在对称轴的右边，y随x的增大而减小，顶点是抛物线的最高点，也就是说当x=0时，y有最大值0。
学以致用、例题解析
例1 已知y=（k+2）x（k²+k-4）是二次函数，且当x＞0时，y随x的增大而增大、
(1)求k的值。
(2)求顶点坐标和对称轴
例2 已知正方形周长为Ccm,面积为S cm²
（1）求S和C之间的函数关系式，并画出图象；
（2）根据图象，求出S=1 cm²时，正方形的周长；
（3）根据图象，求出C取何值时，S≥4  cm2
课堂练习
1.填空：
（1）抛物线y=-5x²,当x=_______时，y有最______值，是__________
（2）当m=______时，抛物线y=(m-1)x m²-m 开口向下
（3）已知函数y=(k²+k)x k²-2k-4是二次函数，它的图象开口________。
2.已知抛物线y=ax2经过点（1,3），求当y=9时，x的值。
3.一个函数的图象是以原点为顶点，y轴为对称轴的抛物线，且过M（-2,2）
（1）求出这个函数的关系式并画出函数图象。
（2）写出抛物线上与点M关于y轴对称的点N的坐标，并求出△MON的面积。