课程内容

《概率的基本性质》
问题提出
1、两个集合之间存在着包含与相等的关系，集合可以进行交、并、补运算，你还记得子集、等集、交集、并集和补集的含义及其符号表示吗？
2、我们可以把一次试验可能出现的结果看成一个集合（如连续抛掷两枚硬币），那么必然事件对应全集，随机事件对应子集，不可能事件对应空集，从而可以类比集合的关系与运算，分析事件之间的关系与运算，使我们对概率有进一步的理解和认识。
知识探究（一）：事件的关系与运算
在掷骰子试验中，我们用集合形式定义如下事件：
C₁={出现1点}，C₂={出现2点}，
C₃={出现3点}，C₄={出现4点}，
C₅={出现5点}，C₆={出现6点}，
D₁={出现的点数不大于1}，
D₂={出现的点数大于4}，
D₃={出现的点数小于6}，
E={出现的点数小于7}，
F={出现的点数大于6}，
G={出现的点数为偶数}，
H={出现的点数为奇数}，等等
思考1：上述事件中哪些是必然事件？哪些是随机事件？哪些是不可能事件？
思考2：如果时间C₁发生，则一定有哪些事件发生？在集合中，集合C₁与这些集合之间的关系怎样描述？
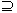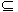一般地，对于事件A与事件B，如果当事件A发生时，事件B一定发生，称事件B包含事件A（或事件A包含于事件B），记为BA（或AB）。
特别地，不可能事件用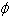表示，它与任何事件的关系约定为：任何事件都包含不可能事件。
思考3：分析事件C₁与事件D₁之间的包含关系，按集合观点这两个事件之间的关系应怎样描述？
思考4：如果事件C5发生或C6发生，就意味着哪个事件发生？反之成立吗？
知识探究（二）：概率的几个基本性质
思考1：概率的取值范围是什么？必然事件、不可能事件的概率分别是多少？
思考2：如果事件A与事件B互斥，则事件A∪B发生的频数与事件A、B发生的频数有什么关系？f_n（A∪B）与f_n（A）、f_n（B）有什么关系？进一步得到P（A∪B）与P（A）、P（B）有什么关系？
思考3：如果事件A与事件B互为对立事件，则P（A∪B）的值为多少？P（A∪B）与P（A）、P（B）有什么关系？由此可得什么结论？
思考4：如果事件A与事件B互斥，那么P（A）+P（B）与1的大小关系如何？