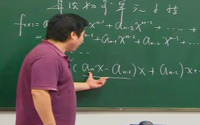课程内容

《算法案例—秦九韶算法》
知识探究（一）：秦九韶算法的基本思想
思考1：对于多项式f（x）=x⁵+x⁴+x³+x²+x+1，求f（5）的值。若先计算各项的值，然后再相加，那么一共要做多少次乘法运算和多少次加法运算？
思考2：在上述问题中，若先计算x²的值然后依次计算x²·x，（x²·x）·x，（（x²·x）·x）·x的值，这样每次都可以利用上一次计算的结果，再将这些数与x和1相加，那么一共做了多少次乘法运算和多少次加法运算？
思考3：利用后一种算法求多项式f（x）=a_nxⁿ+a_n-1x^n-1+……+a₁x+a₀的值，这个多项式应写成哪种形式？
思考4：对于f（x）=（…（（a_nx+a_n-1）x+a_n-2）x+…+a₁）x+a₀，由内向外逐层计算一次多项式的值，其算法步骤如何？
思考5：上述求多项式f（x）=a_nxⁿ+a_n-1x^n-1+……+a₁x+a₀的值的方法称为秦九韶算法，利用该算法求f（x₀）的值，一共需要多少次乘法运算，多少次加法运算？
思考6：在秦九韶算法中，记v₀=a_n，那么第k步的算式是什么？
知识探究（二）：秦九韶算法的程序设计
思考1：用秦九韶算法求多项式的值，可以用什么逻辑结构来构造算法？其算法步骤如何设计？
思考2：该算法的程序框图如何表示？
思考3：该程序框图对应的程序如何表述？
典型例题
例1：已知一个5次多项式为f（x）=5x⁵+2x⁴+3.5x³-2.6x²+1.7x-0.8，用秦九韶算法求f（5）的值。
例2：阅读下列程序，说明它解决的实际问题是什么？
  INPUT “x=”；a
  n=0
  y=0
  WHILE n<5
    y=y+（n+1）*a^n
    n=n+1
  WEND
  PRINT y
  END
小结
秦九韶算法是求一元多项式的值的一种方法，它的特点是：把求一个n次多项式的值转化为求n个一次多项式的值，通过这种转化，把运算的次数由至多n（n+1）/2次乘法运算和n次加法运算，减少为n次乘法运算和n次加法运算，大大提高了运算效率。评价一个算法好坏的一个重要标志是运算的次数，在一元多项式求值的各种算法中，秦九韶算法至今仍是比较先进的算法。