【此视频课程与人教版第24课的知识点相同，同样适用于华师大第28课，敬请放心学习。】

课本内容
《弧长与扇形面积》
学习目标
1.经历探索弧长计算公式及扇形面积计算公式的过程；
2、了解弧长计算公式及扇形面积计算公式，并会应用公式解决问题、
温故而知新
（1）已知·O的半径为R，·O的周长是多少？·O的面积是多少？
（2）什么叫圆心角？
     顶点在圆心，两边和圆相交的角叫做圆心角。
想一想
（1）已知·O的半径为R，1°的圆心角所对的弧长是多少？
     2πR/360=πR/180
（2）n°的圆心角所对的弧长是多少？
     n°的圆心角所对的弧长是n. 2πR/360=πR/180
弧长公式
若·O的半径为R，n°的圆心角所对的弧长1是
l=n.2πR/360=nπR/180
开心练一练：
（1）1°的弧长是______________。半径为10厘米的园中，60°的圆心角所对的弧长是_____________.
（2）如图同心圆中，大圆半径OA、OB交小圆与C、D，且OC ：OA=1 ：2,则弧CD与弧AB长度之比为（   ）
  （A）1 ：1  （B）1 ：2
  （C）2 ：1  （D）1 ：4
例1 制作弯形管道需要先按中心线计算“展直长度”再下料，试计算如图所示的管道的展直长度，即弧AB的长度（精确到0.1mm）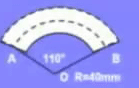

解：∵R=40mm,n=110°
    ∴AB=nπR/180=110/180×π≈76.8（mm）
   因此，所求管道展直长度为76.8mm
想一想
在一块空旷的草地上有一根柱子，柱子上拴着一条长3m的绳子，绳子的一端拴着一条狗(1)这条狗的最大活动区域有多大？
(2)如果这条狗只能绕柱子转过n°的角，那么它的最大活动区域有多大？
什么是扇形？
规定：由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
如何求扇形的面积？
设问：当圆半径一定时，扇形面积的大笑到底和哪些因素有关呢？
想一想：圆心角是 360°的扇形面积是多少？
结论：若字母S表示扇形的面积，n表示圆心角度数，r表示圆半径。
      则计算扇形面积的公式为：
      S扇形=n/360S圆=n/360πr²
弧长公式与扇形的面积公式之间的联系：
扇形中的弧长：L=nπR/180
扇形的面积：S扇形=nπR²/360=nπR/180。R/2
弧长公式与扇形的面积公式之间的联系：
S扇形=1/2LR
（1）当已知弧长L和半径R
     求扇形面积时，应选用S扇形=1/2LR
（2）当已知半径和圆心角的度数，求扇形面积时，应选用S扇形=nπr²/360
例2：已知扇形OAB的半径为12cm。∠AOB=120°。求弧AB的长（结果精确到0.1cm）和扇形OAB的面积（结果精确到0.1cm²）
开心做一做
1.一个扇形的圆心角为90°，半径为2，则弧长=______，扇形面积=_____
2.一个扇形的弧长为20πcm,面积是240πcm²，则该扇形的圆心角为_______________。
3.已知扇形的圆心角为120°，半径为6，则扇形的弧长是（   ）
  A  3π   B 4π    C 5π   D 6π
4.扇形面积大小（   ）
（A）只与半径长短有关
（B）只与圆心角大小有关
（C）与圆心角的大小，半径的长短有关
5、如果半径为r，圆心角为n的n次方的扇形的面积是S，那么n等于（  ）
 （A）360S/ πr  （B）360S/πr²  （C）180S/πr    （D）180S/πr²
6、如果一个扇形面积是它所在圆的面积的1/8,则此扇形的圆心角是（    ）
（A）30°   （B）36°   （C） 45°   （D）60°
小结
1.知识点：弧长、扇形面积的计算公式
2.能力：弧长、扇形面积的计算公式的记忆法
    弧长L=nπR/180    S扇形=nπR²/360=1/2LR