【此视频课程与人教版第24课的知识点相同，同样适用于华师大第28课，敬请放心学习。】

课本内容
《求二次函数的关系式》
一、复习回顾与创新提高
二次函数有几种不同的表达式？
二、实践与探索
例1，已知二次函数的图象经过点A（0，-1）、B（1,0）、C（-1，2），求出对应的二次函数的关系式。
例2 已知抛物线的顶点为（1,-3），且与y轴交于点（0,1），求出此抛物线的关系式。
例3 已知抛物线与x轴交于点（-3,0）、（5,0），且与y轴交于点（0，-3），求出次抛物线的关系式。
推广：若二次函数与x轴的两个交点(x₁,0),(x^₂,0),则二次函数的对称轴还可以表示为：直线x=(x₁+x₂)/2
再推广：若二次函数上两个点位(x₁,y₁)、(x₂,y₂)，且y₁=y₂,由二次函数的对称性可知点(x₁,y₁)与(x₂,y₂)，关于此二次函数的对称轴是对称的，此时，其对称轴也可以表示为：直线x=(x^₁+x^₂)/2
例4 已知抛物线的顶点为(3,-2)，且x轴相交的两交点间的距离为4，求出次二次函数的关系式。
例5 如图所示，求二次函数的关系式。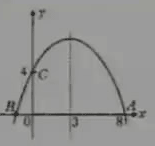

例6 已知抛物线y=ax²+bx+c与抛物线y=-x²-3x+7的形状相同，顶点在直线x=1上，且顶点到x轴的距离为5，求此抛物线的解析式。