【此视频课程与人教版第22课的知识点相同，同样适用于华师大第23课，敬请放心学习。】
课程内容
《二次根式的除法》
复习提问
1、什么叫二次根式？
式子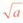
（a≥0）叫做二次根式。
2、三条基本性质：
（1）√a≥0，a≥0（双重非负性）
（2）（√a）2=a（a≥0）
（3）√（a2）=|a|=a（a≥0）或-a（a＜0）
问题：我们知道二次根式的乘法：
√a·√b=√（a·b）（a≥0，b≥0）
类似地猜想√a/√b，应怎样计算呢？a、b的取值范围是怎样的？为什么？
探究一：计算下列各式，观察计算结果，你发现什么规律？
（1）√4/√9=（ ），√（4/9）=（ ）
（2）√16/√49=（ ），√（16/49）=（ ）
（3）√2/√3____√（2/3） √2/√5____√（2/5）
规律：√a/√b=√（a/b）（a≥0，b＞0）
二次根式除法法则：两个二次根式相除，等于把被开方数相除，作为商的被开方数。
例4：计算
（1）√24/√3 （2）√（3/2）÷√（1/18）
解：（1）√24/√3=√（24/3）=√8=√（4×2）=2√2
（2）√（3/2）÷√（1/18）=√（3/2÷1/18）=√（3/2×18）=√（3×9）=3√3
试一试
计算：
注意：如果被开方数是带分数，应先化成假分数。
如果根号前有系数，就把系数相除，仍作为二次根号前的系数。
探究二：商的算术平方根有什么性质？
√（a/b）=√a/√b（a≥0，b＞0）
商的算术平方根等于被除式的算术平方根除以除式的算术平方根。
例5：化简
（1）√（3/100） （2）√（25x/9y2）
例6：计算
（1）√3/√5 （2）（3√2）/√27 （3）√8/（√2a）
在二次根式的运算中最后结果一般要求：
（1）被开方数中不含分母
（2）被开方数不含能开得尽方的因数或因式
满足什么条件的二次根式是最简二次根式：
（1）被开方数不含分母。
（2）被开方数不含能开得尽方的因数或因式。
总结
1、利用商的算术平方根的性质化简二次根式。
2、二次根式的除法计算有两种常用方法：
（1）利用公式：√a/√b=√（a/b）（a≥0，b＞0）
（2）把除法先写成分式的形式，在进行计算或化简。
3、在进行计算或化简时，可以把能化简的二次根式先化简，再考虑如何化去分母中的根号。
