课程内容

《用二分法求方程的近似解》
学生活动：
问题1：能否求解以下几个方程
（1）x²-2x-1=0
（2）2x=4-x
（3）x³+3x-1=0
（4）lgx=3-x
指出：用配方法可求得方程x²-2x-1=0的解，但此法不能运用于解另外的方程。
问题2：不解方程，如何求方程x2-2x-1=0的一个正的近似解（精确到0.1）？
画出y=x²-2x-1的图象。
可得：方程x²-2x-1=0一个根x₁在区间（2,3）内，另一个根x₂在区间（-1,0）内。
由此可知：借助函数f（x）=x²-2x-1的图象及其单调性，我们发现f（2）=-1＜0，f（3）=2＞0，这表明此函数图象在区间（2,3）上穿过x轴一次，可得出方程在区间（2,3）上有唯一解。
问题3：能否描述二分法？
    对于在区间[a,b]上连续不断，且f（a）f（b）＜0的函数y=f（x），通过不断地把函数f（x）的零点所在的区间一分为二，使区间的两端点逐步逼近零点，进而得到零点（或对应方程的根）近似解的方法叫做二分法。
问题4：二分法实质是什么？
    用二分法求方程的近似解，实质上就是通过“取中点”的方法，运用“逼近思想逐步缩小零点所在的区间”。
例1：借助电子计算器或计算机用二分法求方程2^x+3x=7的近似解（精确到0.1）。
探究：
为什么由|a-b|＜ε，便可判断零点的近似值为a（或b）？
总结：
1、利用（1）图像法；（2）函数状态法，寻找确定近似解所在的区间[a,b]，验证f（a）·f（b）＜0；
2、不断二分解所在的区间，即取区间（a,b）的中点x1=（a+b）/2
3、计算f（x₁）：
   ①若f（x₁）=0，则x₀=x₁
   ②若f（a）·f（x₁）＜0，则令b=x₁（此时x0∈（a,x₁））
   ③若f（b）·f（x₁）＜0，则令a=x₁（此时x0∈（x₁,b））
4、判断是否达到给定的精确度，若达到，则得出近似解；若未达到，则重复步骤2-4。
练习：
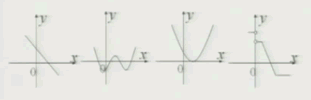
下列函数的图像与x轴均有交点，其中不能用二分法求其零点的是（   ）

课堂小结
1、明确二分法是一种求一元方程近似解的常用方法。
2、二分法求方程的近似解的步骤，以及计算机（器）的使用，让我们感受到程序化的方法即算法的价值。
3、尝试对二分法进行编程，通过计算机来求方程的近似解。